Substitue y=mx4 into the circle equation x^2 (mx4)^2 = 2 (mx4) Find all m that gives exactly 1 solution for x You can use completing the square for x to get the formula in theClick here👆to get an answer to your question ️ A circle S = 0 passes through points of intersection of circles x^2 y^2 2x 4y 1 = 0 and x^2 y^2 4x 2y 5 = 0 and cuts the circle x^2Match the values in this circle to those of the standard form The variable represents the radius of the circle, represents the xoffset from the origin, and represents the yoffset from origin Step
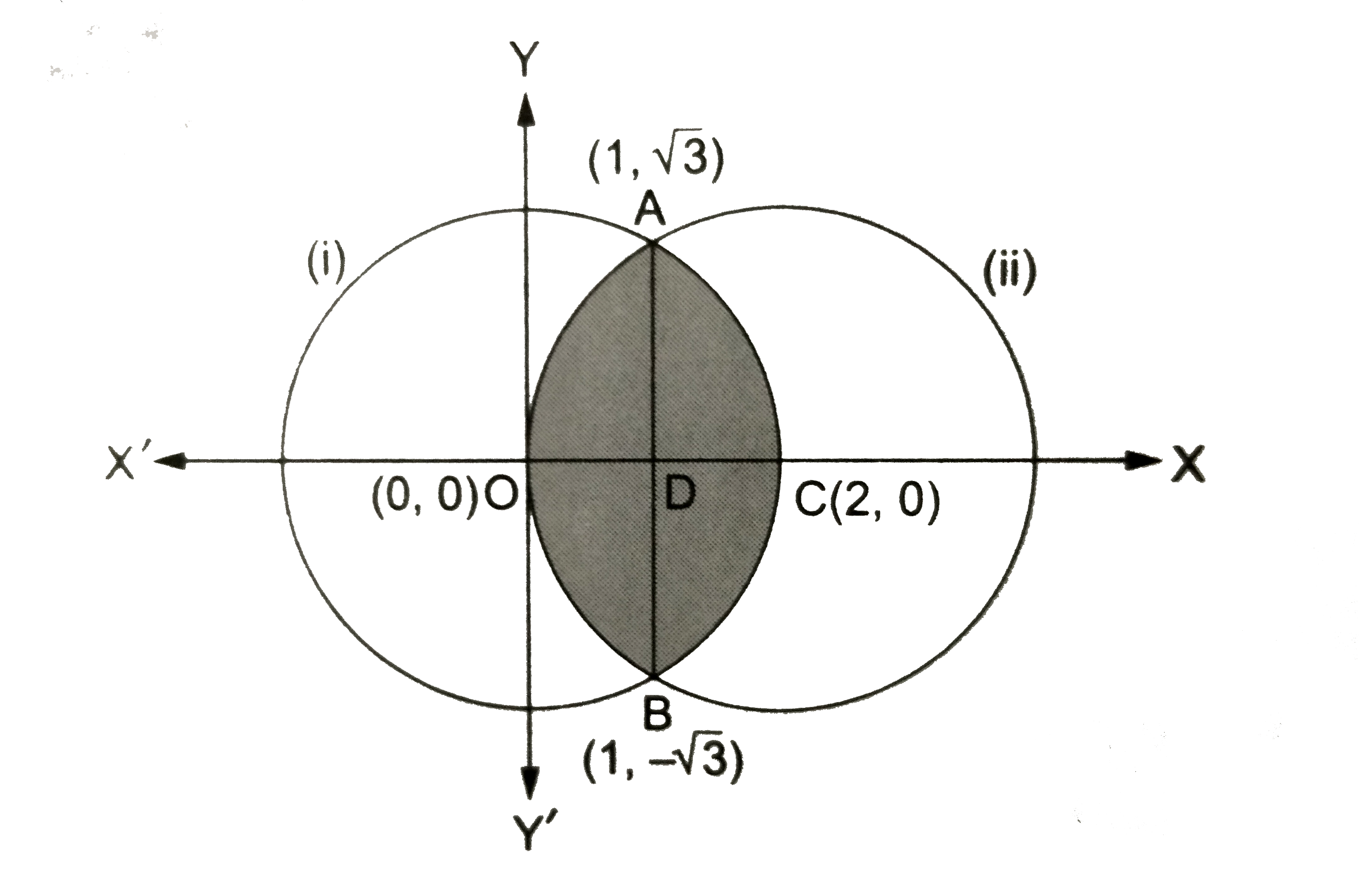
Using Integration Find The Area Of The Region Enclosed Between The Two Circles X 2 Y 2 4 And X 2 2 Y 2 4 Sarthaks Econnect Largest Online Education Community
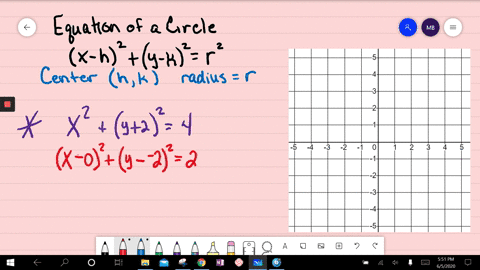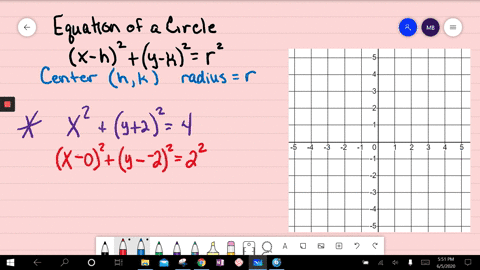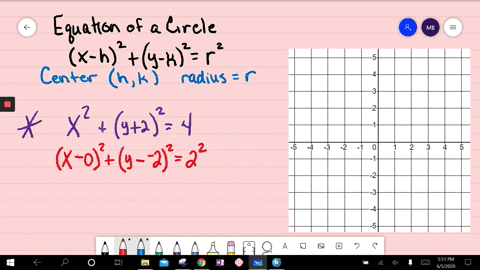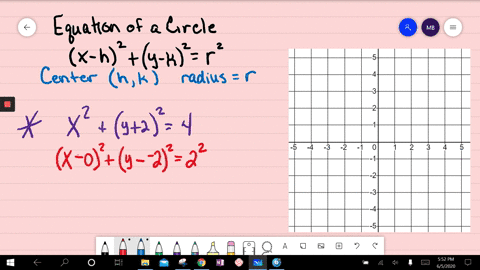
X^2+y^2=4 circle
X^2+y^2=4 circle-Free PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystep(x−2)2 y2 = 4 ( x 2) 2 y 2 = 4 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2 Match the values in this




The Lines Parallel To Normal To The Curve Xy 1 Is Are
The general equation of a circle is #(xa)^2(yb)^2=r^2# The center is #(a,b)# and the radius is #r# #(x2)^2(y1)^2=2^2# This is a circle, center #(2,1)# and radius #=2# MarkThe circles x^{2}y^{2}xy=0 and x^{2}y^{2}xy=0 intersect at an angle (a) \frac{\pi}{2} (b) \frac{\pi}{3} (c) \frac{\pi}{6} (d) \frac{\pi}{4}Watch the fuIf any circle touches the coordinate axes, then radius of circle is equal to the perpendicular distance from centre to the coordinate axes Equation of circle is x 2 y
The line y = x intersects the circle x 2 y 2 − 8 x − 4 y 10 = 0 at P and Q Find a) the coordinates of P and Q b) the equation of the circle with PQ as the diameterClick here👆to get an answer to your question ️ The circle x^2 y^2 = 4 cuts the circle x^2 y^2 2x 4 = 0 at the points A and B If the circle x^2 y^2 4x k = 0 passes through A and B thenMatch the values in this circle to those of the standard form The variable represents the radius of the circle, represents the xoffset from the origin, and represents the yoffset from origin Step
(x 2)2 (y − 4)2 = 9 ( x 2) 2 ( y 4) 2 = 9 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2View solution steps Solve for y y = − ( (6 − x) (x 2) 4) y = (6 − x) (x 2) − 4, x ≥ −2 and x ≤ 6 View solution steps Graph Quiz Algebra (x−2)2 (y 4)2 = 16 Similar Problems from Web SearchAt any point (x (1),y (1)) on the circle The slope of the tangent will be dy/dx = (y)/x = m Edit m = x/y ,sorry I




Ex 8 1 12 Mcq Area Bounded By Circle X2 Y2 4 And Lines X 0




Solved Find The Center And Radius Of Each Circle X 2 2 Chegg Com
Comparing this to the standard form above, we can see that a = 2 and b = 4 (watch out for those negative signs y – (4) is the same as y 4) So, the center of the circle is (a, b) = (2, 4)Graph (x3)^2(y4)^2=4 Step 1 This is the form of a circle Use this form to determine the center and radius of the circle Step 2 Match the values in this circle to those of the standardAlgebra Graph x^2y^2=1 x2 y2 = 1 x 2 y 2 = 1 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2



Solution Find An Expression For The Top Half Of The Circle X 2 Y 2 2 4




The Equation Of A Circle Is X 2 Y 2 4 The Centre Of The Smallest Circle Touching This Circle And The Line X Y 5 2 Has The Condition
Originally Answered what is the tangent to the circle whose equation is x^2y^2=4?Answer (1 of 5) \text {Writing both in standard form, whatever that is, we have } x^2y^2=2^2 \text { and }(x2)^2y^2=2^2 So we are find the area common to two congruent circles each passing




Let E Be The Ellipse X 2 9 Y 2 4 1 And C Be The Circle X 2 Y 2 9 Let P And Q Be The Points 1 2 And 2 1 Respectively Then




The Line 2x 3y 1 Intersects The Circle X 2 Y 2 4 At A And B If The Equation Of The Circle On Ab As Diameter Is X 2 Y 2 2gx 2fy C 0 Then C
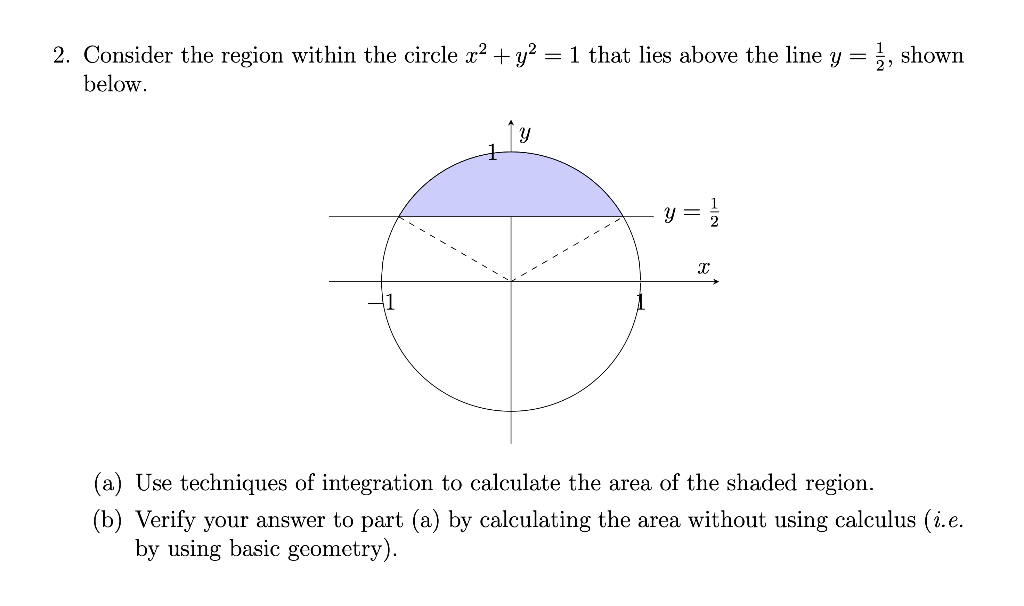



Solved 2 Consider The Region Within The Circle X2 Y2 1 Chegg Com



Q Tbn And9gcqiju7t6 Gnncnbepsaicrufw5wsdug79ufzsek6r 4a271mwvjv 5 Usqp Cau




For The Points On The Circle X 2 Y 2 2x 2y 1 0 The Sum Of The Maximum And Minimum Values Of 4x 3y Is




Tangent To The Circle X 2 Y 2 4 At Any Point On It In The First Quadrant Makes Intercept Oa Youtube




Using Integration Find The Area Of The Region Enclosed Between The Two Circles X 2 Y 2 4 And X 2 2 Y 2 4 Sarthaks Econnect Largest Online Education Community




Graphing Functions Rough Sketch Of The Circle X 2 Y 2 8x And The Parabola Y 2 4x Mathematics Stack Exchange



Circle Equations Lesson Article Khan Academy




Circle With Centre 0 4 And Passing Through The Projection Of 2 4 On X Axis Is Youtube




Normal To The Circle X 2 Y 2 4 Divides The Circle Having Centre At 2 4 And Radius 2 In The Ares Of Ratio Pi 2 3pi 2 Then The Normal Can Be
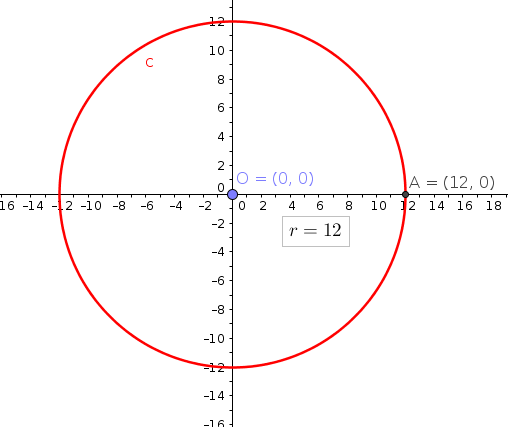



How Do You Find The Center And Radius Of The Circle Given X 2 Y 2 144 Socratic




A Tangent Pt Is Drawn To The Circle X 2 Y 2 4 At The Point P Sqrt3 1 A Straight Line L Youtube
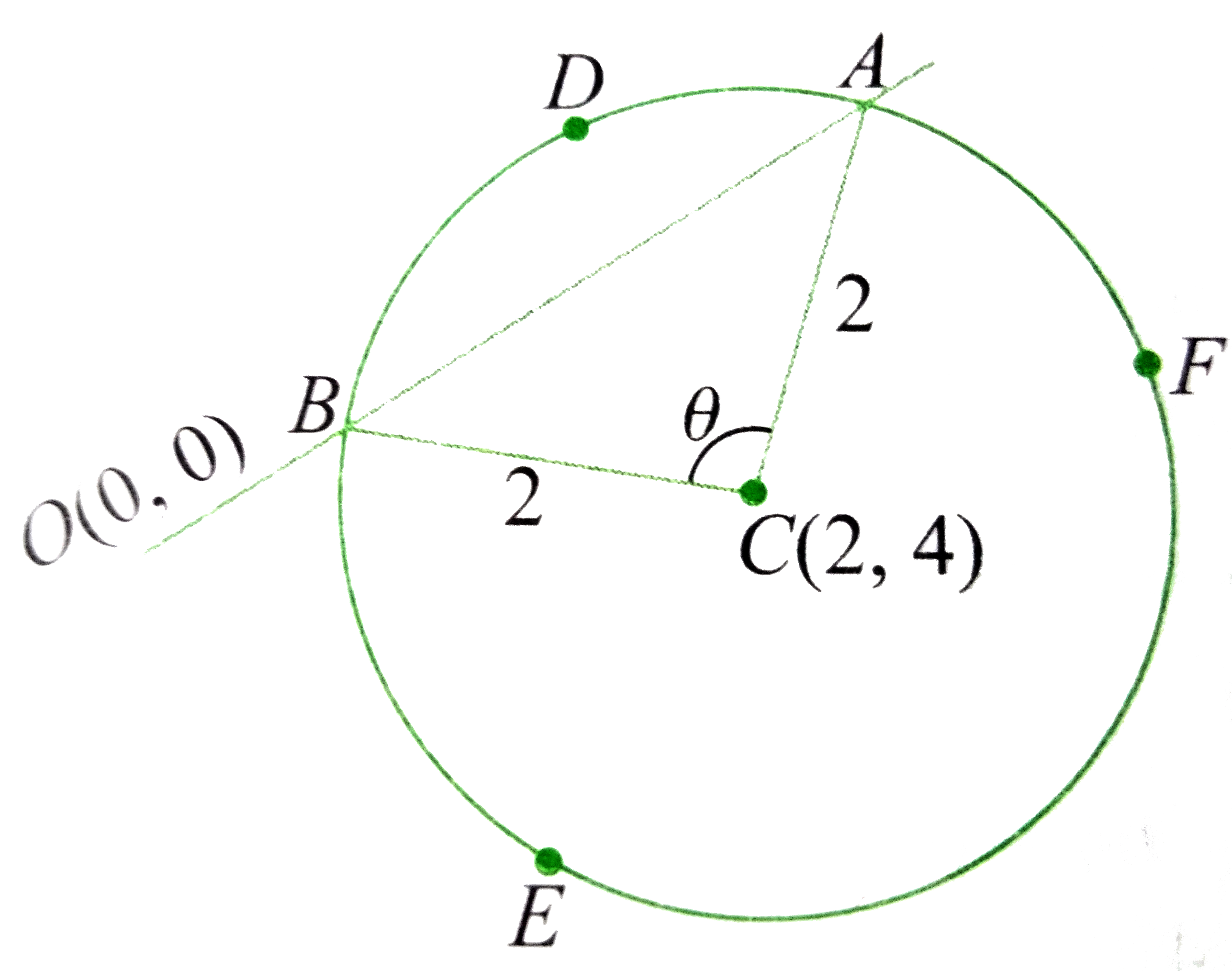



Normal To The Circle X 2 Y 2 4 Divides The Circle Having Centre At 2 4 And Radius 2 In The Ares Of Ratio Pi 2 3pi 2 Then The Normal Can Be



Graphing This Circle Equation X 2 Y 2 14x 4y 0 Mathskey Com
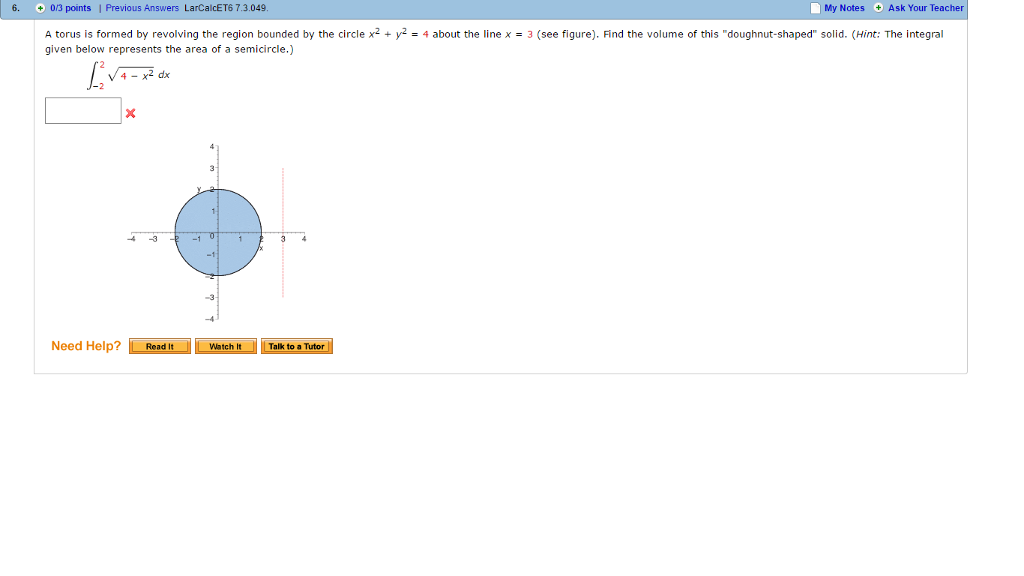



Solved A Torus Is Formed By Revolving The Region Bounded By Chegg Com




The Nearest Point On The Circle X 2 Y 2 6x 4y 12 0 From 5 4 Is




What Is The Equation Of The Circle Shown In The Graph X 3 2 Y2 4 X 3 2 Y2 2 X2 Y Brainly Com




The Equation Of The Tangents To The Circle X 2 Y 2 4 Which Are Parallel To X 2y 3 0 Are




Ex 8 2 6 Mcq Smaller Area Enclosed By Circle X2 Y2 4 Line



Find The Foci Of The Graph Of X 2 4 Y 2 9 1 Mathskey Com




The Line 2x 3y 1 Intersects The Circle X 2 Y 2 4 At A And B If The Equation Of The Circle On Ab As Diameter Is X 2 Y 2 2gx 2fy C 0 Then C
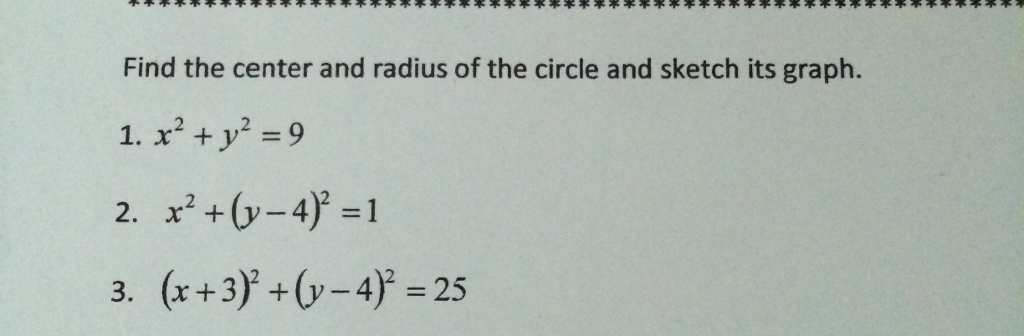



Solved Find The Center And Radius Of The Circle And Sketch Chegg Com
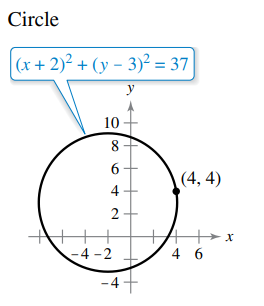



Answered Circle X 2 Y 3 37 Y 10 8 Bartleby




How Do You Graph X 2 Y 2 4 Socratic




Ex 8 2 6 Mcq Smaller Area Enclosed By Circle X2 Y2 4 Line




Smaller Area Enclosed By The Circle X 2 Y 2 4 And The Lines X Y 2 Is Youtube




The Equation Of The Tangents To The Circle X 2 Y 2 4 Which Are Parallel To X 2y 3 0 Are




Multivariable Calculus Region D Is Bounded By Below By Z 0 And Above By X 2 Y 2 Z 2 4 And On Sides X 2 Y 2 1 Is Required To Be Setup In Spherical Coordinate Mathematics Stack Exchange



What Is The Area Between Two Circles X Y 2 4 And X 2 Y 2 4x Quora




Find The Centre And Radius Of The Circles X 2 Y 2 4x 8y 45 0 Youtube



How To Find The Area Of The Portion Of The Circle X 2 Y 2 4 Cut Off By The Line X 2y 2 In The First Two Quadrants Quora
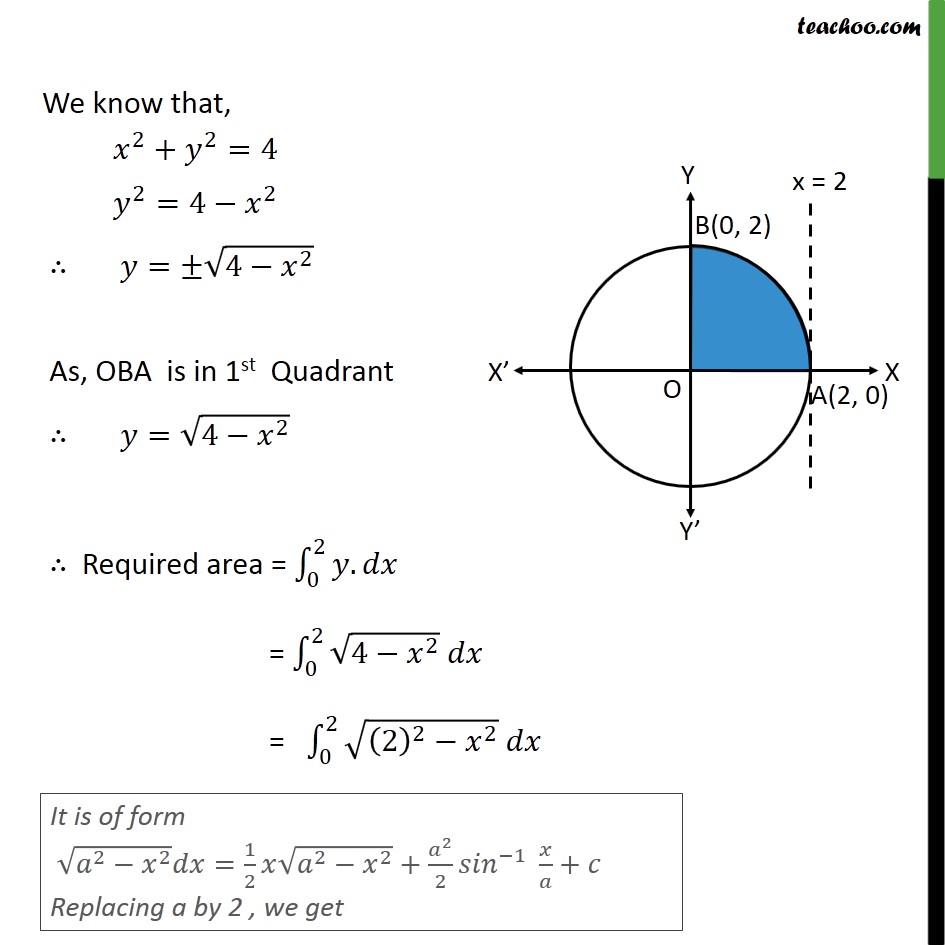



Ex 8 1 12 Mcq Area Bounded By Circle X2 Y2 4 And Lines X 0
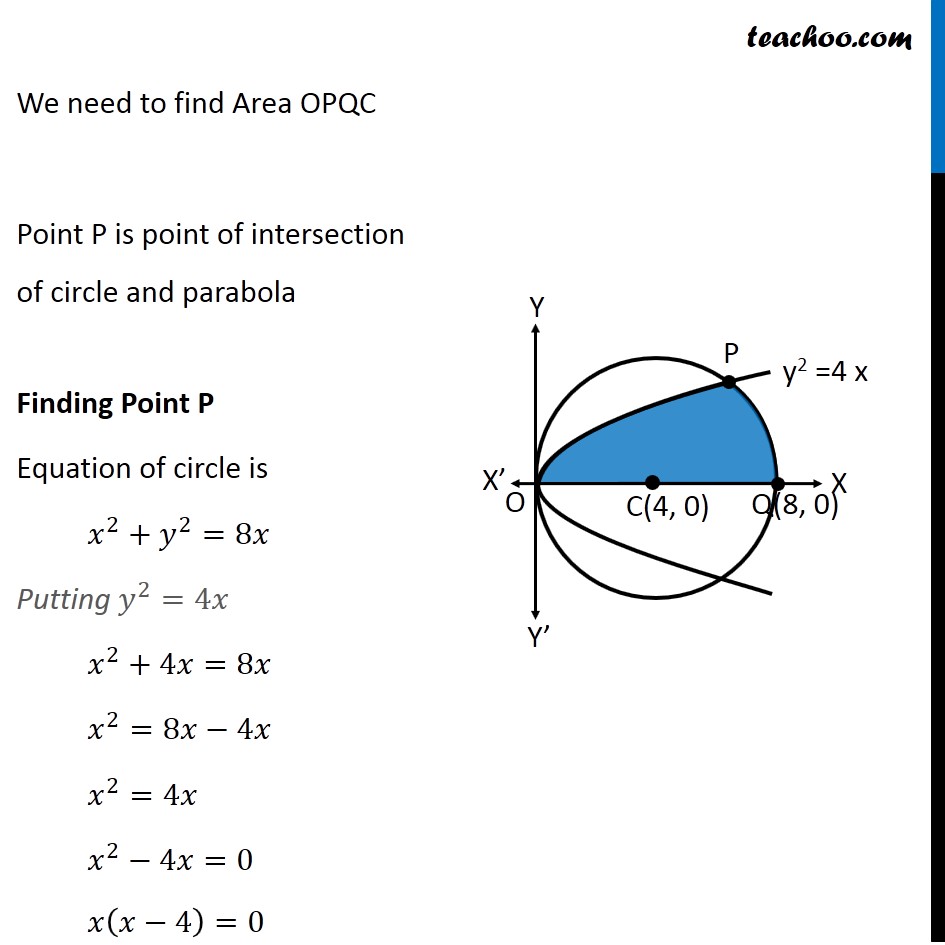



Example 7 Find Area Lying Above X Axis Included B W Circle




What Is The Standard Form Of The Equation Of The Circle In The Graph A X 1 2 Y 2 2 4 B Brainly Com




Find Area Of Region Bounded By Curves X 2 Y 2 4 Y 3x And X Axi
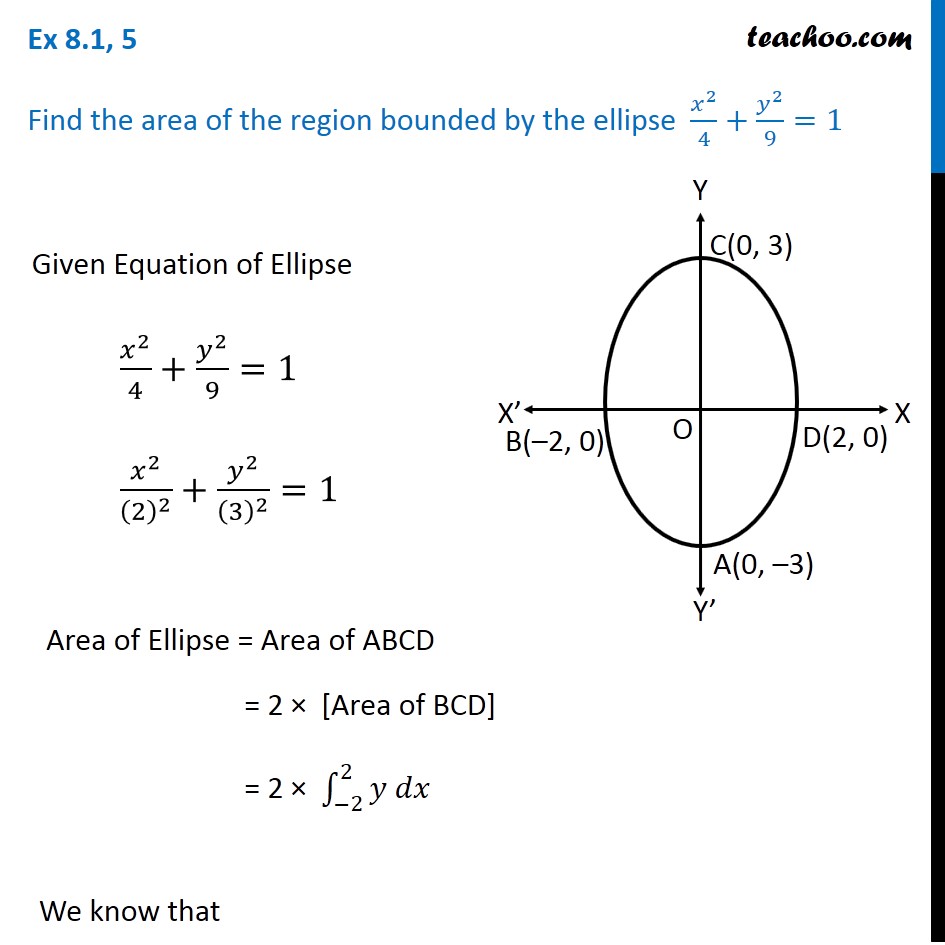



Ex 8 1 5 Find Area By Ellipse X2 4 Y2 9 1 Class 12



Solved Find The Center And Radius Of The Circle X 3 2 Chegg Com
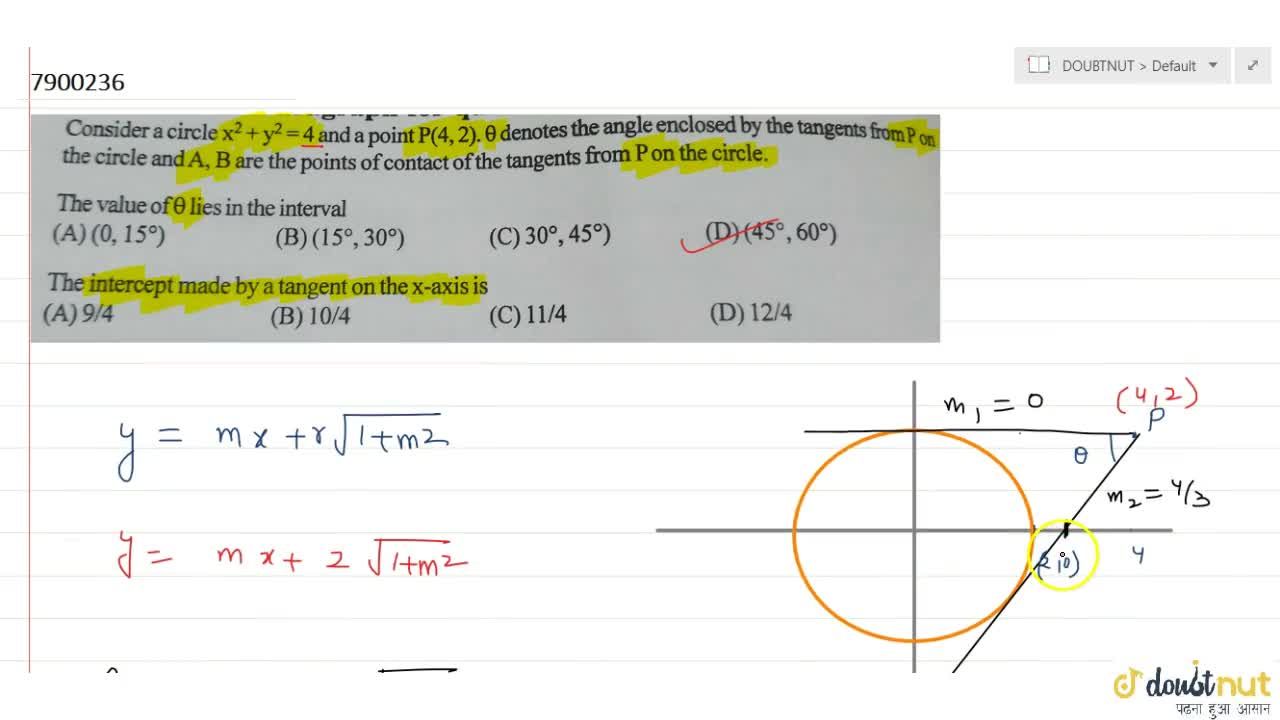



Consider A Circle X 2 Y 2 4 And A Point P 4 2 8 Denotes The Angle Enclosed By The Tangents From P On The Circle And A B Are The Points Of Contact Of The Tangents




A Circle Touches The Y Axis At 0 2 And Has An Intercept Of 4 Units On The Positive Side Of The X Axis Then The Equation Of The Circle Is
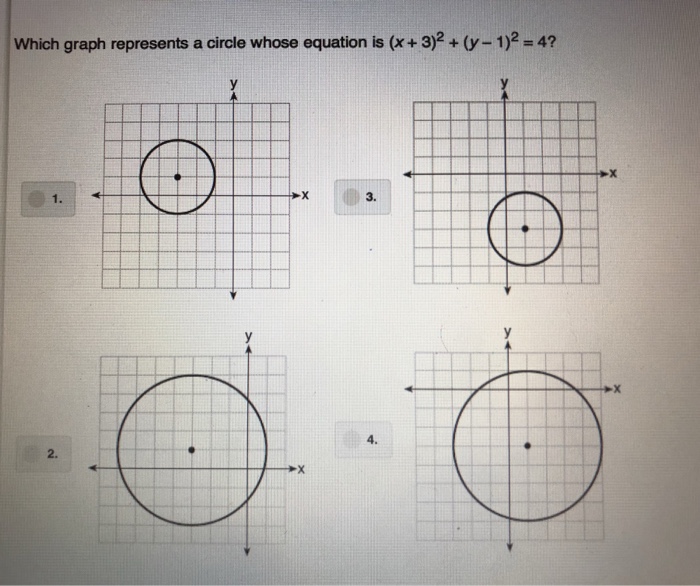



Solved Which Graph Represents A Cirale Whose Equation Is X Chegg Com



What Is The Equation Of Tangent And Normal Of The Circle X 2 Y 2 4 At 1 3 1 2 Quora




The Coordinates Of The Centre Of The Smallest Circle Touching The Circle X 2 Y 2 4 And The Lines X Y 5 2 Are




Find The Centre And Radius Of The Circle X 2 Y 2 6x 8y 24 0




Solved 4 Find The Standard Form Of The Equation Of The Chegg Com
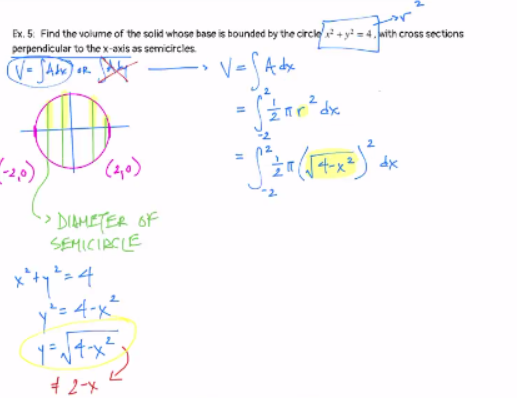



Solved Can Someone Finish This Problem Find The Volume Of Chegg Com



Smaller Area Enclosed By The Circle X 2 Y 2 4 And The Line X Y 2 Is Sarthaks Econnect Largest Online Education Community




Example 10 Find Area Enclosed Between Two Circles X2 Y2 4




Find The Equations Of The Tangents To The Circle X 2 Y 2 4x 4y 4 0 At The Point 4 2




Find The Smaller Area Enclosed By The Circle X2 Y2 4 And The Line X Y Maths Application Of Integrals Meritnation Com




Which Equation Represents A Circle With The Same Center As The Circle Shown But With A Radius Of 2 Brainly Com




Find The Smaller Area Enclosed By The Circle X 2 Y 2 4 And The Line X Y 2




Example 10 Find Area Enclosed Between Two Circles X2 Y2 4




The Equation Of The Tangent Of Circle X 2 Y 2 4x 4y 4 0 Which Make Equal Intercepts On The Positive Co Ordinate Axis Is




Find The Parametric Representation Of The Circle X 2 Y 2 2x 4y 4 0




The Tangent To The Circle X 2 Y 2 4x 2y K 0 At 1 1 Is X 2y 1 0 Then K




Geometry Is The Circle X 2 2 Y 4 2 4 Tangent To The X Axis The Y Axis Mathematics Stack Exchange




Sketch The Circles Y 2 X 2 1 And Y 2 X 3 2 4 There Is A Line With A Positive Slope That Is Tangent To Both Circles Determine The




Sketch The Surface X 2 Y 2 4 Homework Study Com




Find The Image Of The Circle X 2 Y 2 2x 4y 4 0 In The Line 2x 3y 5 0 Youtube



Exercises Involving Distance And Circles



How To Determine If X 2 Y 2 4 Is A Function Quora




Obtain The Parametric Equation Of The Circle Represented By X 2 Y 2 4




View Question 1 The Equation Of A Circle Is X 2 Y 2 4x 2y 11 0 What Are The Center And The Radius Of The Circle Show Your Work
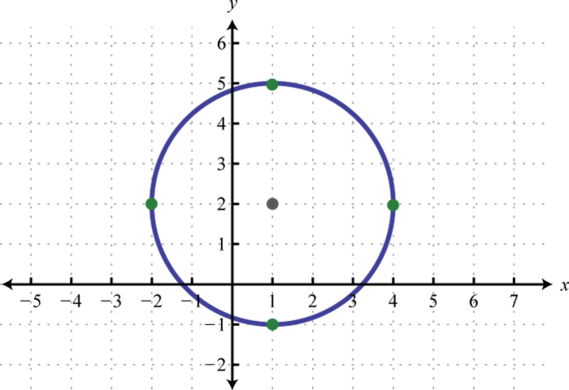



Circles




Solved Find An Expression For The Function Whose Graph Is The Given Curve The Top Half Of The Circle X 2 Y 2 2 4




Week 4 Point C 2 4 Lies On A Circle X2 Y2 8x 6y Ppt Download




Find The Equation Of The Circle Passing Through The Points Of Intersection Of The Circles X 2 Y 2 2x 4y 4 0 And X 2 Y 2 10x 12y 40 0 And Whose Radius Is 4




The Common Tangent To The Circles X 2 Y 2 4 And X 2 Y 2 6x 8y 24 0 Also Passes Through The Point




Solved Let C Be The Bottom Half Of The Circle X 2 Y 2 4 Chegg Com
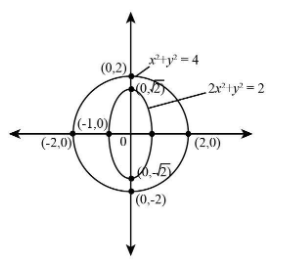



Find Common Tangent Of X2 Y2 4 And 2x2 Y2 2 Is Class 12 Maths Cbse



The Common Tangent To The Circles X 2 Y 2 4 And X 2 Y 2 6x 8y 24 0 Also Passes Through The Point Sarthaks Econnect Largest Online Education Community




Two Circles X 2 Y 2 2x 4y 0 And X 2 Y 2 8y 4 0 A Touch Each Other Externally Youtube




Graph X 2 Y 2 4 Youtube



Q Tbn And9gcqm Sck6bfmyzpj2bmaosgzrrxmcqdgwf2teaddjkcwtgd1z6vlj Cg Usqp Cau




A Circle Cutting The Circle X 2 Y 2 4 Orthogonally And Having Its Centre On The Line 2x 2y 9 0 Passes Through Two Fixed Points These Points Are



Q Tbn And9gcqhyre3n2dulx4x1 C Fskxhrvkics65nmupcptjjyde9d Eyscr1j Usqp Cau
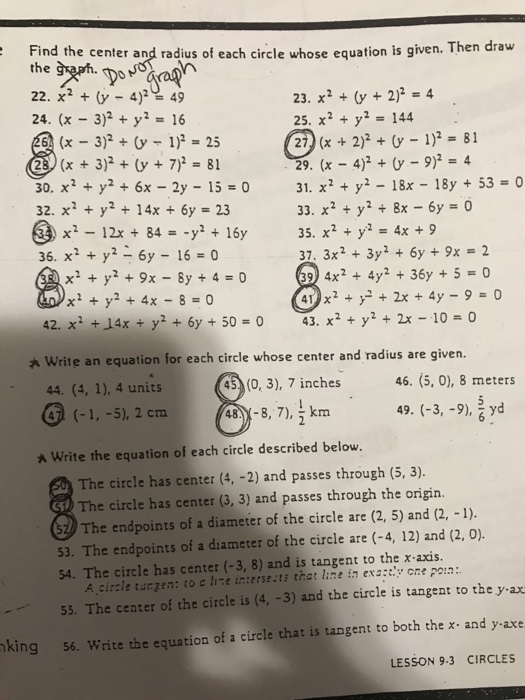



Solved Find The Center And Radius Of Each Circle Whose Chegg Com
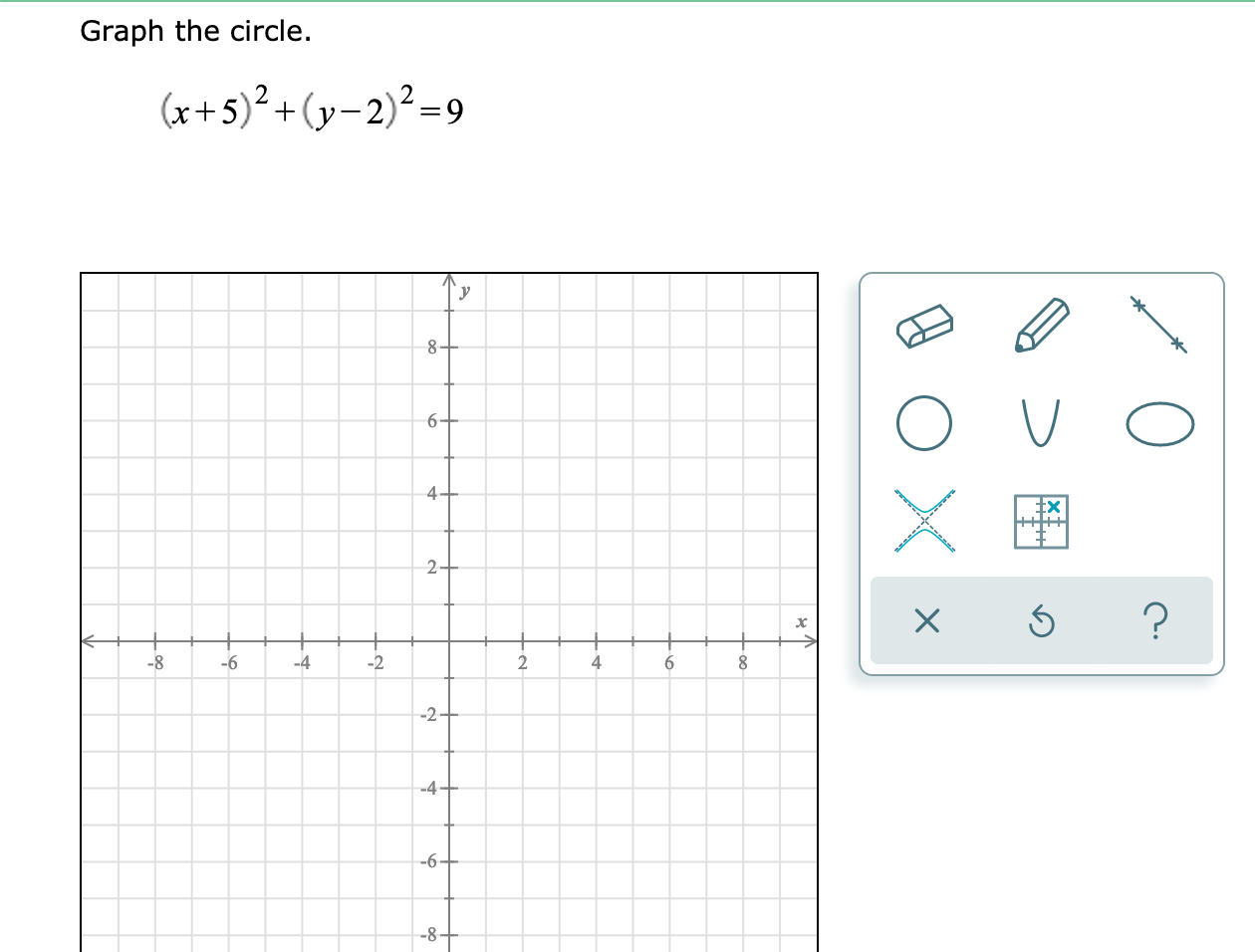



Solved Graph The Circle X 5 2 Y 2 2 9 Y 8 6 O Ox 4 X Chegg Com




The Lines Parallel To Normal To The Curve Xy 1 Is Are
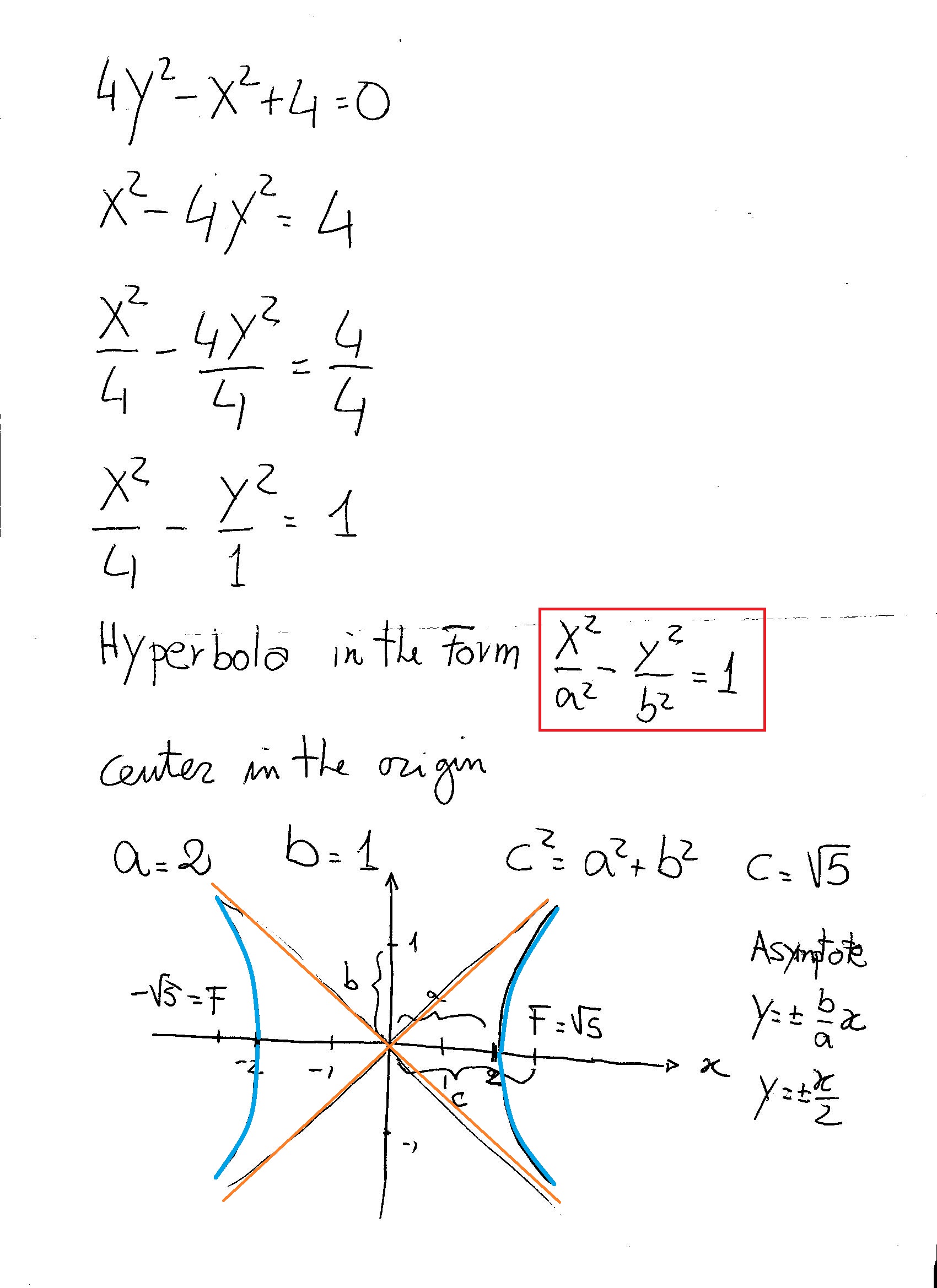



How Do You Identity If The Equation 4y 2 X 2 4 0 Is A Parabola Circle Ellipse Or Hyperbola And How Do You Graph It Socratic



Consider The Circles S1 X 2 Y 2 4 And S2 X 2 Y 2 2x 4y 4 0 Which Of The Following Statements Are Correct Sarthaks Econnect Largest Online Education Community



Area Lying In The First Quadrant And Bounded By The Circle X 2 Y 2 4 And The Lines X 0 And X 2 Is Sarthaks Econnect Largest Online Education Community



Solved Graph Each Equation X 2 Y 2 100




Solved Let S Be The Hemisphere X 2 Y 2 Z 2 4 Z 0 Chegg Com
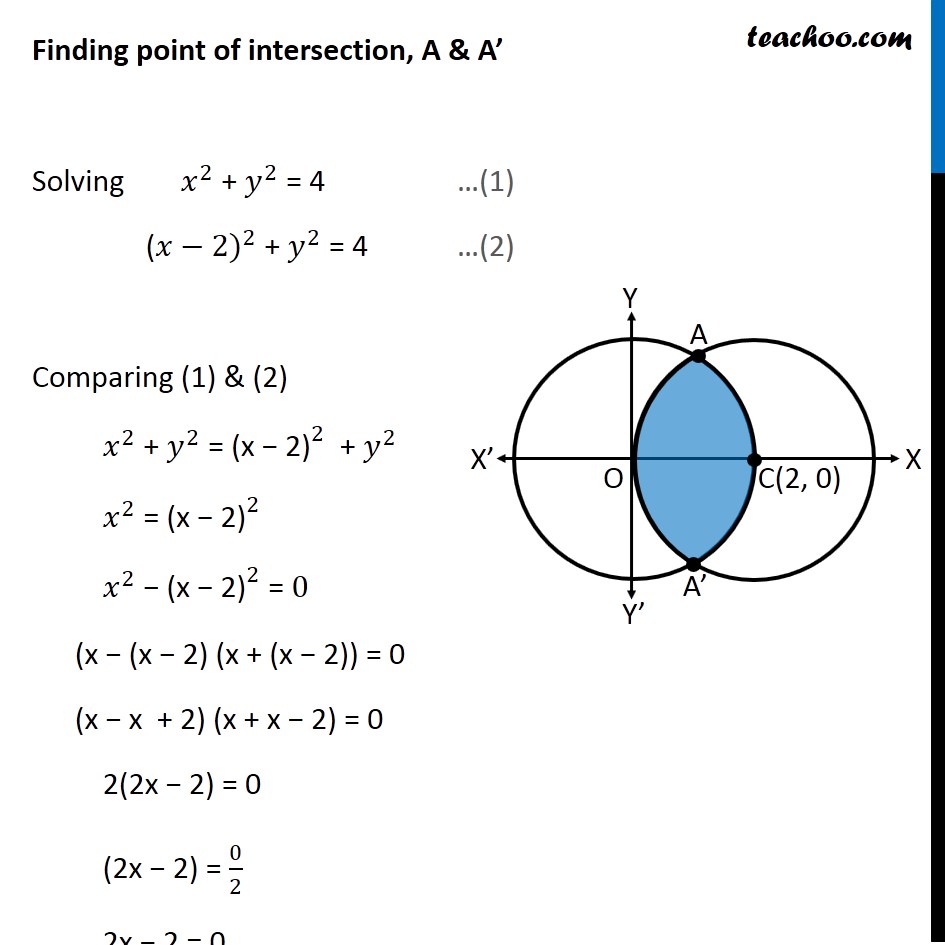



Example 10 Find Area Enclosed Between Two Circles X2 Y2 4




Solved Give The Boundary Of The Set S X Y 1 X2 Y Chegg Com




Circle Centre A B Radius R Ppt Download



Q Tbn And9gctuuqz3lj7bhnqrjxdcajs3hzj21db8a4gu3qqrn1pke3b1wzl33inm Usqp Cau



Tangent To The Circle X 2 Y 2 4 At Any Point On It In The First Quadrant Makes Intercepts Oa And Ob On X And Y Axes Respectively Sarthaks Econnect




Consider The Circles C1 X 2 Y 2 2x 4y 4 0 And C2 X 2 Y 2 2x 4y 4 0 And The Line L X 2y 2 0 Then




Obtain The Parametric Equation Of The Circle Represented By X 2 Y 2 4




10 1 Circles 1 X Y R Higher Maths Lessons Mrthomasmaths X2 Y2 R2 X 2 Y 2 R 2 Youtube




Find The Centre And Radius Of Each Of The Circle I X 2 Y 2 2x 4y 4 0 Ii 4x 2 4y 2 24x 8y 24 0




Draw A Circle With An Equation Of X 2 Y 2 4y 5 Homework Study Com




Find The Point Of The Hyperbola X 2 24 Y 2 18 1 Which Is Nearest To The Line 3x 2y 1 0




Find The Length Of Direct Common Tangent Of Circle X 1 2 Y 2 2 4 And X 5 2 Y 2 2 1




Example 10 Find Area Enclosed Between Two Circles X2 Y2 4
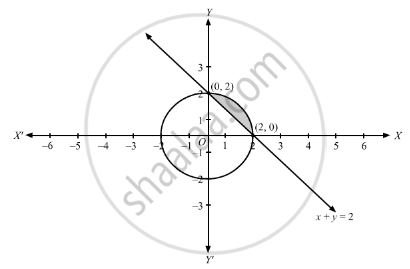



Find The Area Of The Region X Y X2 Y2 4 X Y 2 Mathematics Shaalaa Com




Toppr Ask Question



0 件のコメント:
コメントを投稿