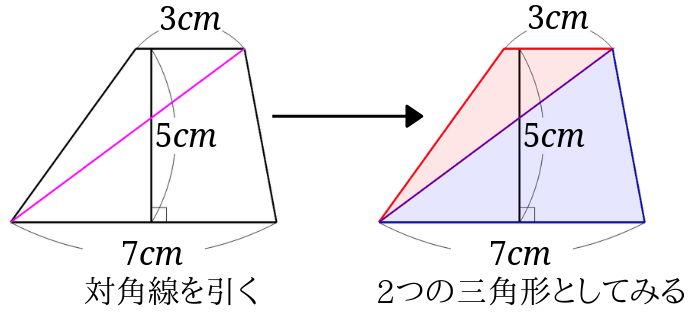
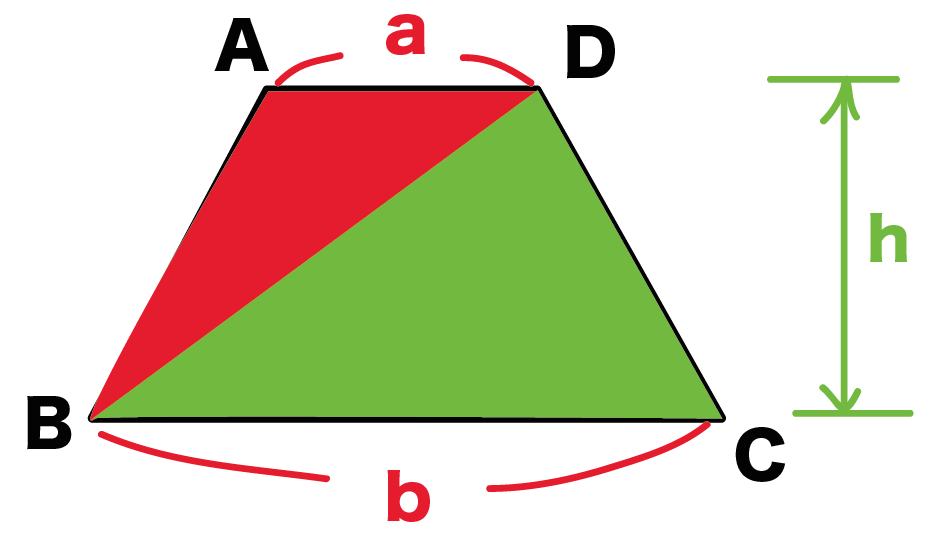
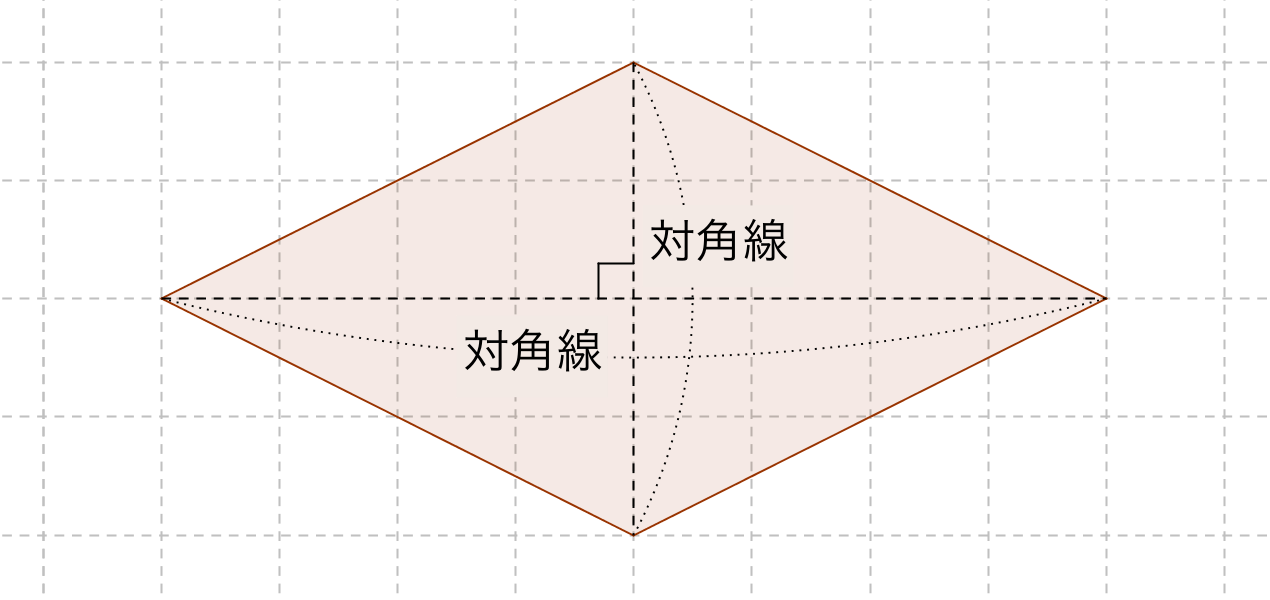
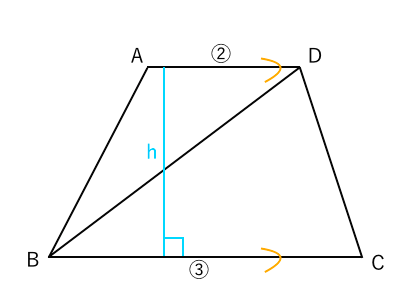
①上底のさかさまの三角形と ②下底のふつうの三角形。 三角形の面積の出し方は 底辺×高さ÷2 ①なら 上底×高さ÷2 ②なら 下底×高さ÷2 台形の面積は①②なので それを簡略化したら (上 なぜ対角線をかけるの? ひし形の面積を求めるのに、なぜ対角線を掛けるのか? それはね ひし形の面積を求めるために次のような図形を考えているからなんだよ! 対角線を引くと、ひし形は4つの三角形に分けられるんだけど、それらの三角形をパタンと折り返します。 すると、こんな感じになるよね。 これをすべての三角形でやると このように長方形を作る台形の性質 性質①同側内角の和が 180° 性質②1 本の対角線がなす 2 つの三角形の面積比は (上底) (下底) 性質③2 本の対角線がなす上下の三角形は相似 性質④2 本の対角線がなす左右の三角形の面積が等しい
台形の面積の公式 算数の公式
台形 面積 求め方 なぜ
台形 面積 求め方 なぜ-包含関係の式からもわかるとおり、台形の面積の求め方で、等脚台形の面積は求められます。 台形の面積=(上底+下底)×高さ÷2 高さの情報が無い場合は、この式では求まりませんね。 三角形の3辺の長さから面積を求めるものとして、ヘロンの公式というものがあります。 私のブログの今回は対角線の長さが分かっている時のひし形の面積の求め方を説明していきます。 \(2\)つの方法で説明することができるので、ぜひ小学生のお子さんに教える際などに参考にしてください。 目次 ひし形の面積の公式;




5年算数 台形の面積 指導実践 ネコ好きな学校の先生の日常
T:a=底面の面積 b=上面の面積 c=aとbの真中の面積 h=高さ とすると、 Sor という公式がある。この公式は、台の体積はおろか、三角形の面積まで求めることができる。 例えば、台形、半球を求めてみよう。 半球の体積=(πr 2 +3/4πr 2 3台形の3辺と高さから、残りの1辺と面積を求めます。 モード 上底 or 下底を求める 斜辺を求める h 高さ a or c 上底/下底のどちらか b 斜辺 d 斜辺 a 上底 台形近似の考え方 S = ∫ a b f (x) d x S=\displaystyle\int_a^bf(x)dx S = ∫ a b f (x) d x を求める問題を考えます。 定積分の値を台形の面積(の和)で近似してみましょう。数値積分(計算が難しい定積分の値を近似的に求める)が主なモチベーションです。
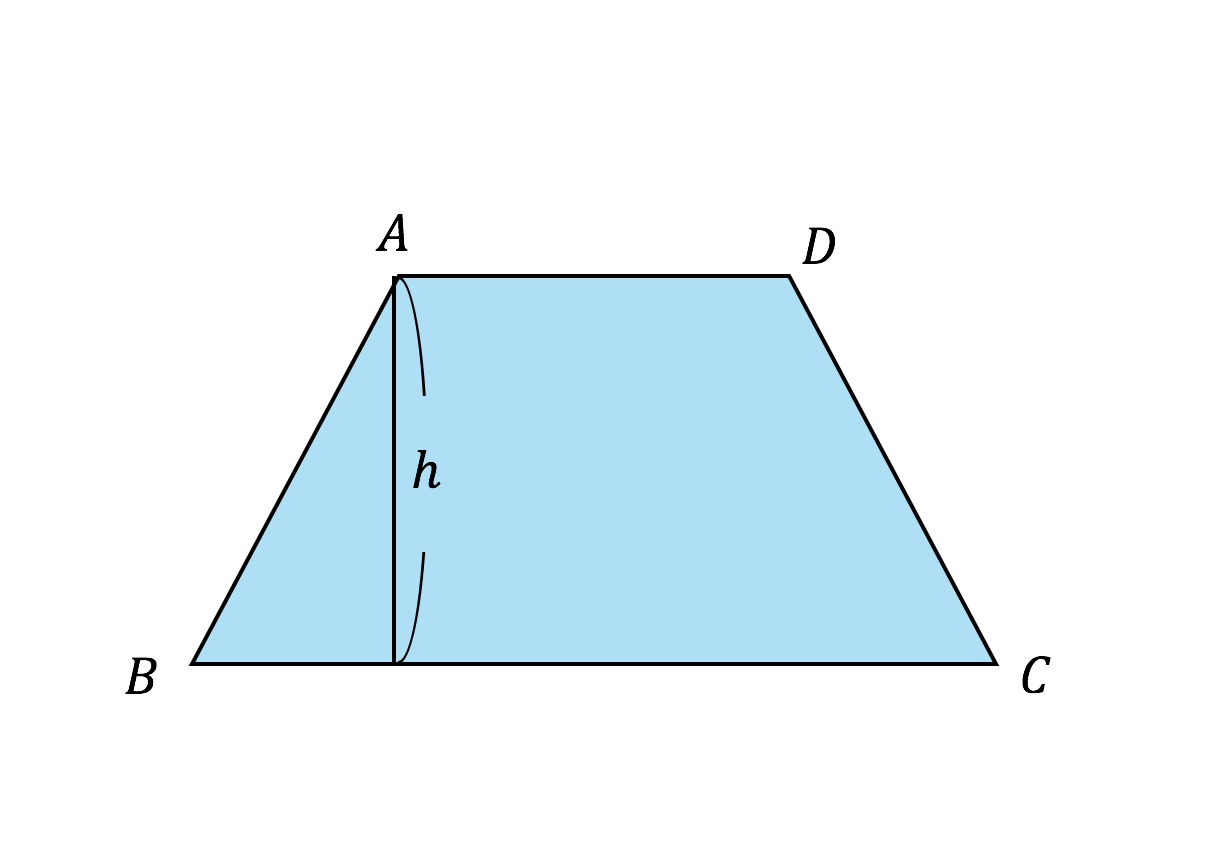
ア 三角形、平行四辺形、ひし形及び台形の面積の求め方を考えること。 〔算数的活動〕(1)イ 三角形、平行四辺形、ひし形及び台形の面積の求め方を、具体物を用いたり、 言葉、数、式、図を用いたりして考え、説明する活動 第4学年では、長方形と正方形の面積の学習において、1cm2角錐・円錐の体積の求め方には底面積×高さ÷3という公式があります。 「なぜ、÷3するのか」という疑問を解決するために、四角錐などの立体を組み合わせて考えました。 自分たちが体積を求められる立体になるように、くっつけ方を考え、「÷3」の理由を導き出しました。 6年担任 與座 幹太 この台形の面積は\((ADBC)×h×\frac{ 1 }{ 2 }\)になります。 一般化して台形の面積は、 (上底下底)×(高さ)×\(\frac{ 1 }{ 2 }\) で求めることができます。 では次にどうしてこうなるのかを紹介します。 台形の面積の公式の証明(2種類) 次に 台形の面積の公式の証明 に入ります。
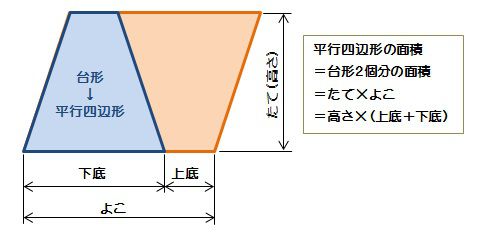
1.はじめに ~なぜ「台形の面積の求め方」なのか~ ひし形及び台形の面積の求め方は,今回の学習指導要領の改訂で,5年生に新たに追加された指導内容の1つである。 これまでもひし形や台形の面積については求めることを扱ってはきたが,「面積の求め方を考える」つまり「面積をどのように求めたらよいのかと考え,公式化する」ことまでは扱ってはいなかっ台形断面の等流計算 開水路の等流計算には、次のマニングの公式がよく用いられる。 (式-2) 補足 (上底+下底)×高さ÷2 で上底= として整理する。 ここで、各記号は次のことを示している。 n:粗度係数(水路壁面、底面の粗さを示す値で、水路の平行四辺形の面積=底辺×高さより, 台形を2つ合わせた平行四辺形の面積=(上の辺十下の辺)×高さとなる。 台形の面積は,この平行四辺形の面積の半分なので, 台形の面積=(上の辺+下の辺)×高さ÷2 となる。上の図で台形の面積は,




なぜ台形の面積は 上底 下底 高さ 2なの Youtube



台形の面積は公式が分からなくても大丈夫 対角線を引いたり等積変形を利用したりする求め方とは みけねこ小学校
台形の面積の求め方が 相変わらず、毎日、毎日、ルワンダの算数の教科書を見ています。 さらっと見ていると日本との違いが分からないのですが、じっくり見ると結構見えてきます。 なかなか面白いです。 今日は、台形の面積の所を見ていました。平行四辺形になるので面積は、(上底+下底) 高さです。 台形二つ分なので「÷2」を追加します。 よって台形の面積を求める公式「(上底+下底) 高さ÷2」になります。 指針(考え方) この円柱の側面積= 球の表面積の公式と同じ式をしていることが分かる. あなたは今、球の表面積を求める公式を知らないものとします. 円柱の側面積=球の表面積 を示すことによって, (円柱の側面積= なので,) 球体の表面積= を示すことができます. 輪切りの考え



1




三角形の面積の公式 2 って どうして2で割るの
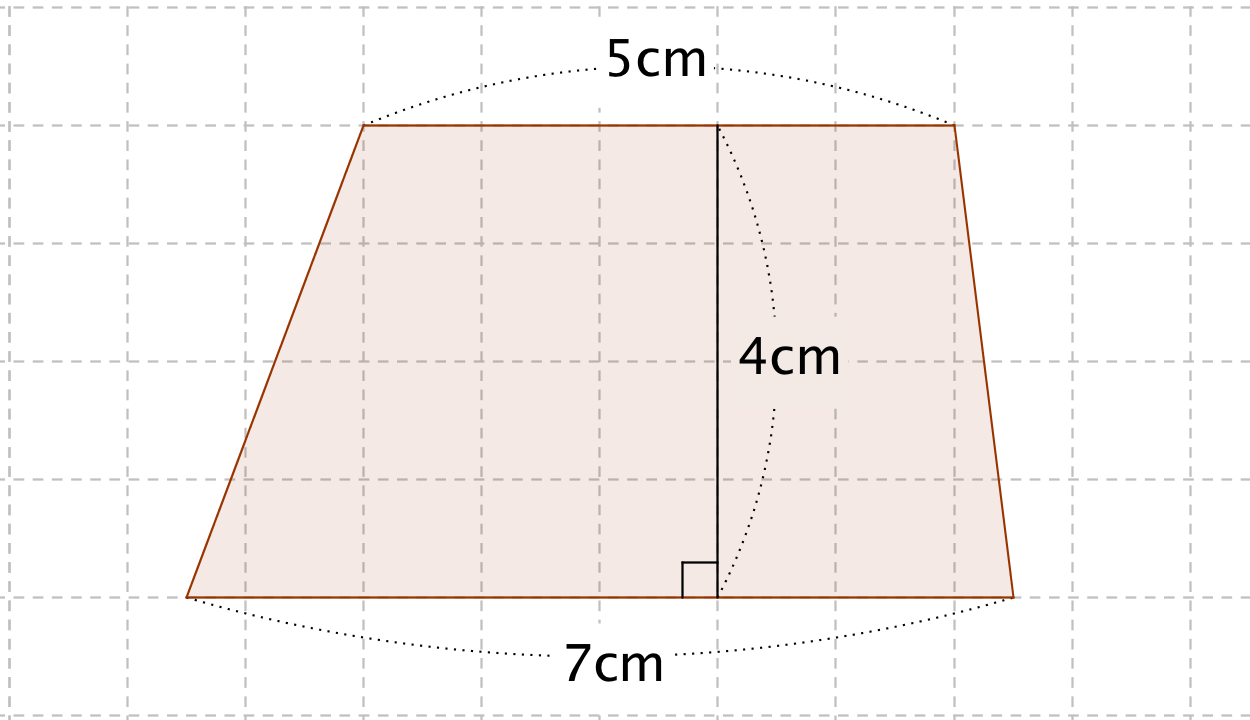
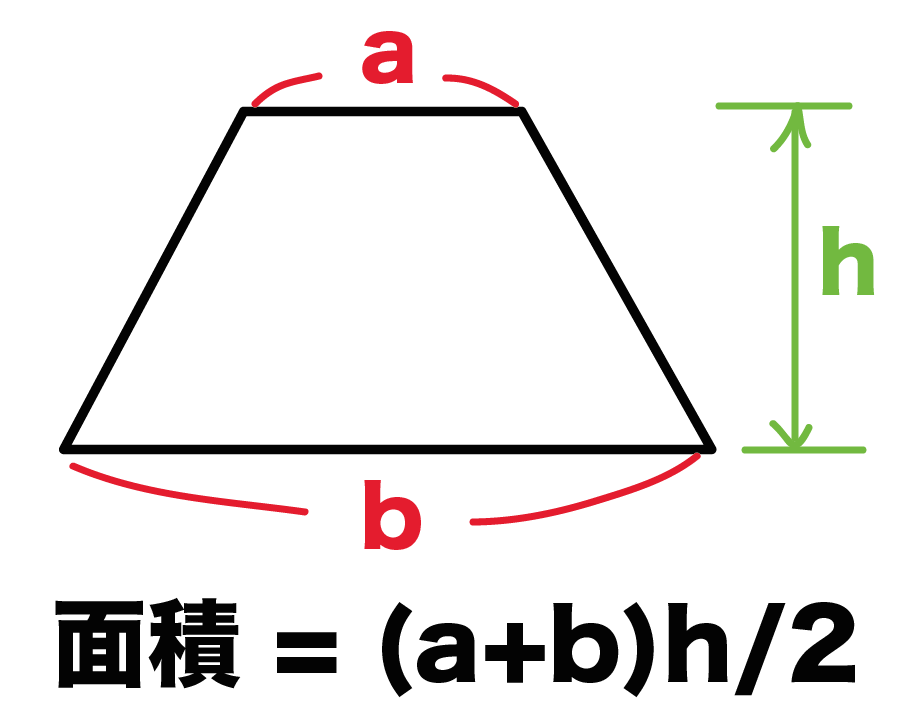
右図の緑色で塗りつぶした台形部分の面積を求めなさい。 円Oの半径は8cmとします。 画像クリックでもう少し大きく見れます。 ヒント 考えすぎるとドつぼにはまります! とは言っても、考えないと手が出ませんし、考えすぎる子の考えの中にもヒントがあります。 有名過ぎる面積問題9題台形の面積の公式 台形の面積は 『(上底下底)×高さ÷2 ÷ 2 』 で求めることができます。 たとえば以下のような問題の場合。 例題 上底3cm、下底7cm、高さ6cmの台形の面積を求めよ。 答えはこのように求めることができます。 (3 7)× 6÷2=30(cm2) ( 3 7) × 6 ÷ 2 = 30 ( c m 2) なぜ台形がこのような公式で求めることができるのか、その理由を見ていきましょう。底面積(ていめんせき)とは、立体の底面の面積です。 立体の形状の違いで底面積の求め方が違います。 例えば、円柱の底面積は半径×半径×314です。 立方体の底面積は、縦×横で計算しましょう。 今回は底面積の意味、求め方、円錐、三角錐、四角柱



3分で分かる 台形の面積の求め方 公式についてわかりやすく 合格サプリ




台形の面積の求め方 公式が誰でも一目でわかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ
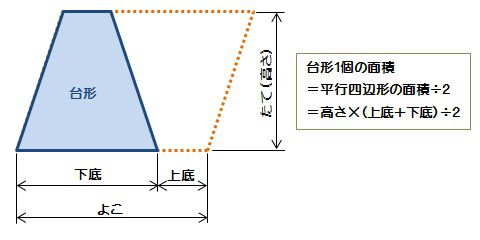
台形の面積を求める公式は、s = {(上底)(下底)}×(高さ)÷2 で表されます。このページでは、台形の面積の求め方を、計算問題と共に説明しています。また、公式の導き方も説明しています。今、求めたいのは台形1個分の面積ですよね? まとめると 台形2個を合体させた平行四辺形の面積は、高さ×(上底+下底) 求めたいのは台形1個の面積 こうなります。つまり、 台形1個分の面積=平行四辺形の面積÷2 と考えればいいのです。 なので、 台形の面積=(上底+下底)×高さ÷2 となるの台形の底辺と計算(求め方)、上辺の関係 台形の底辺は、 高さ 面積 上底(または下底) が既知のとき計算できます。これは台形の面積を求める式が、 台形の面積=(上底下底)×高さ÷2 のためです。実際に、下図の台形の底辺(下底)を計算します。



数学 本質 三角形の面積の公式はなぜああなる そもそも面積とは Torm Note




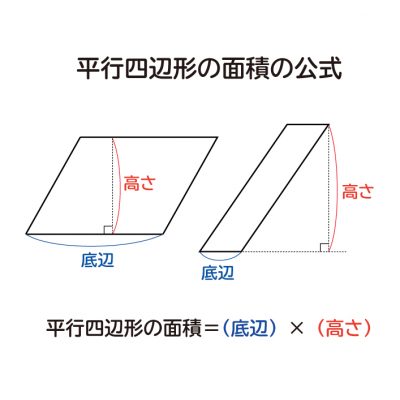
平行四辺形の面積の求め方 公式と計算例
台形の面積の求め方 このq&aは「進研ゼミ小学講座」の会員向けコンテンツを一部公開したものです。 回答内容は、小学生の学習範囲を考慮して制作されています。 面積台形の面積 2 )となっています。 2 )ではまちがいですか? 台形の面積=(上底下底)×高さ÷2ですね。 平行な2つの辺 多角形の面積の求め方 長方形=縦×横 正方形=1辺×1辺=対角線×対角線÷2 平行四辺形=底辺×高さ 台形=(上底+下底)×高さ÷2 ひし形(対角線直交四角形)の面積=対角線×対角線÷2 三角形=底辺×高さ÷2 円の面積の求め方三角形の面積(3辺からヘロンの公式) 三角形の面積(1辺と2角から) 正方形の面積 長方形の面積 台形の面積 台形の高さ・面積(4辺の長さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 平行四辺形の面積(底辺と高さから)



台形の面積 算数の公式覚えてますか



都立中高一貫校受検 絶対合格 のために家族で頑張るブログ 台形の面積の公式がなぜそうなるのか を考えてみよう
いろいろな台形の面積の求め方を教えて 無断複製・転載・翻訳を禁ず GAKKEN B Title 算数 Author VAIO Created Date PM公式の考察 なぜ? 台形の面積の公式が「 上底 下底 高さ ( 上 底 下 底) × 高 さ ÷ 2 」になるのかを考えてみましょう。 「赤色の台形」と同じ形の「青色の台形」をひとつ用意します。 「青色の台形」をひっくり返して、「赤色の台形」とくっつけると 平行四辺形になりますね。 平行四辺形の面積を求める公式 は 平行四辺形の面積 底辺 高さ 平 行 四 辺次の図形の黒くぬった部分の面積を求めなさい。 → 解答 問題2 次の図形の黒くぬった部分の面積を求めなさい。 → 解答 問題3 次の図形の黒くぬった部分の面積を求めなさい。 → 解答 問題4 三角形ABCの面積が85c㎡のとき、三角形ADEの面積を求めなさい。ただし、辺BCは5等分されています



台形の公式は必要か




平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun
まとめ:台形の体積の求め方は「上 – 下」!! 台形の体積(正四角錐台)の体積の求め方はどうたった?? 大きな正四角錐から小さいやつをひけばいい んだ。 補助線をひいて正四角錐をみつけてみよう。 そんじゃねー Ken Ken Qikeruの編集・執筆をしています。 「教科書、もうちょっとその1 台形を2倍にして平行四辺形を作り,その半分の面積と考える。 これですんなり,台形の面積をもとめる公式が となるのが分かりますね。 その2 台形を2つの三角形に分けて,それぞれの三角形の面積をもとめて合計する。




高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




台形公式について 次の問題で なぜ F X 0ではなく なぜ F X Okwave




台形の面積は公式が分からなくても大丈夫 対角線を引いたり等積変形を利用したりする求め方とは みけねこ小学校



台形の面積 算数の公式覚えてますか



台形の面積公式 算数と図形 理数系無料オンライン学習 Kori
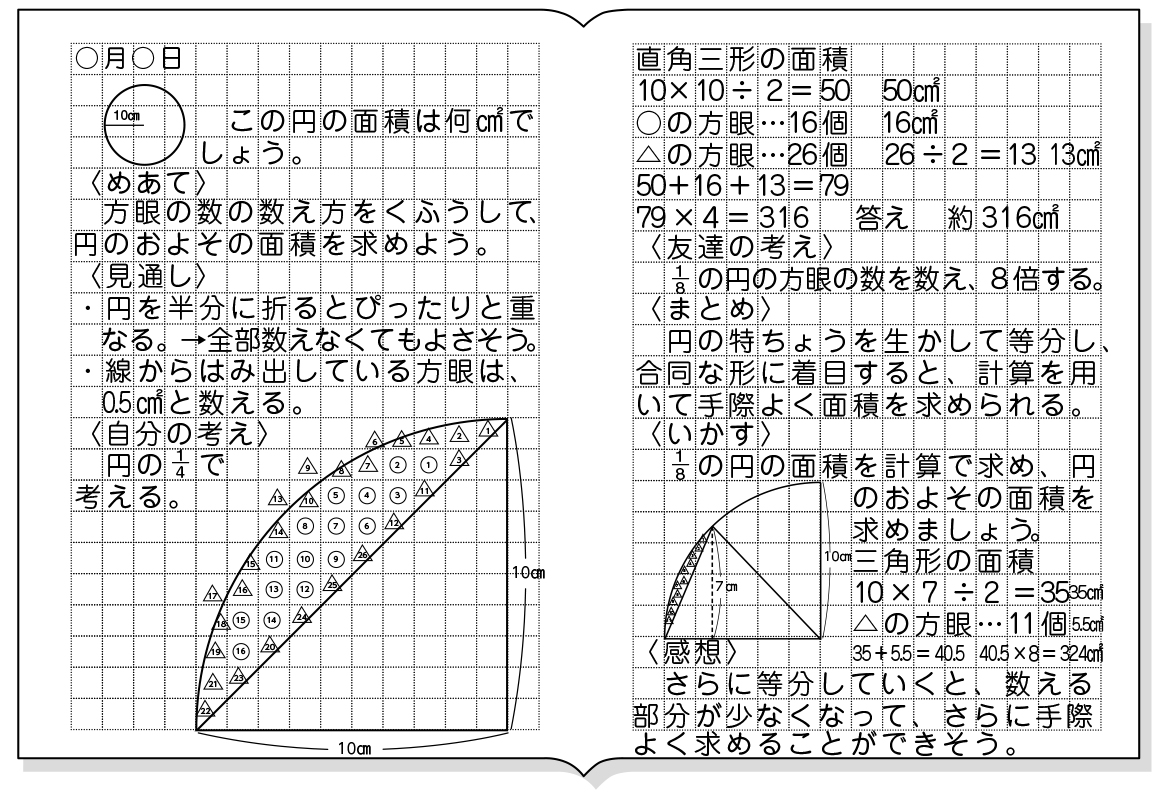



小6算数 円の面積 指導アイデア 1 みんなの教育技術
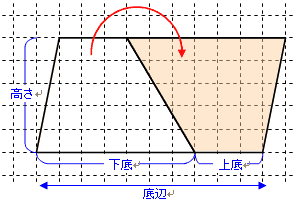



面積の考え方 算数の教え上手 学びの場 Com



三平方の定理 台形の面積の求め方なんですが なぜ2 10なんでしょう Yahoo 知恵袋




三角形の面積を求める方法は何通り その1 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog




5年算数 台形の面積 指導実践 ネコ好きな学校の先生の日常




簡単公式 台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
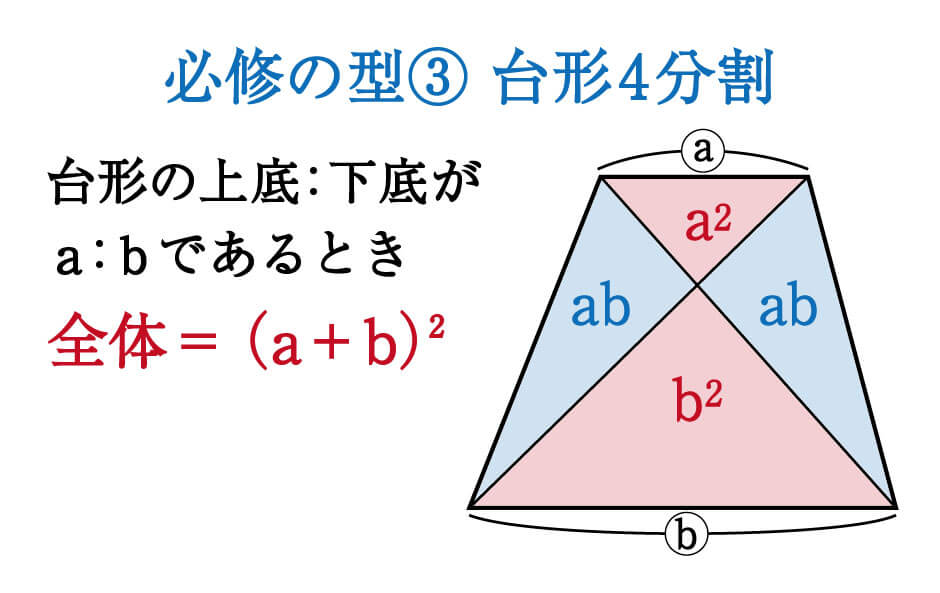



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



正方形の面積は 1分でわかる公式 対角線 ルートの関係 面積から辺の長さを求める方法
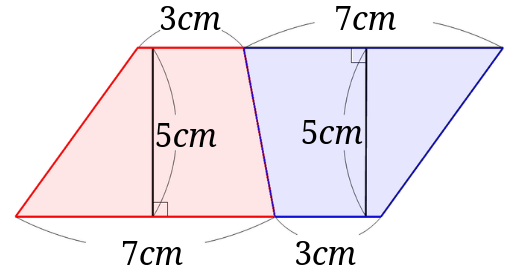



台形の面積は公式が分からなくても大丈夫 対角線を引いたり等積変形を利用したりする求め方とは みけねこ小学校
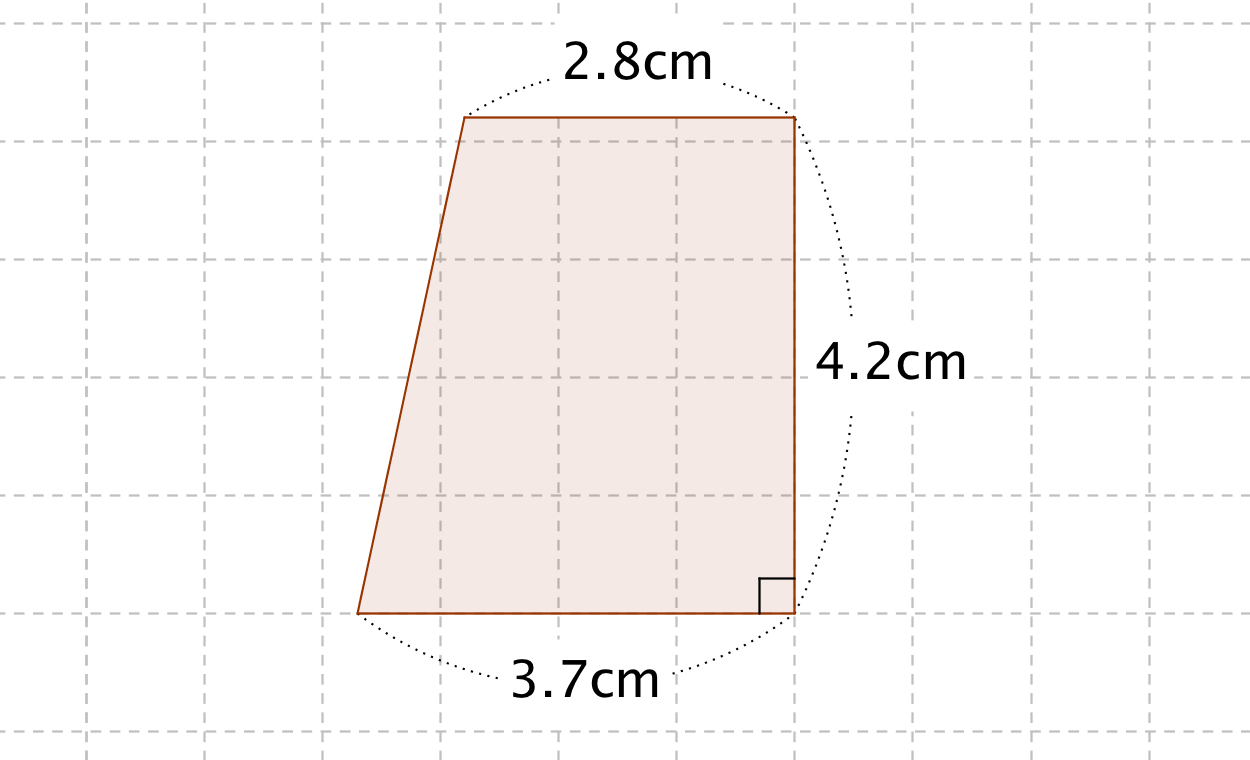



台形の面積の公式 算数の公式



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典
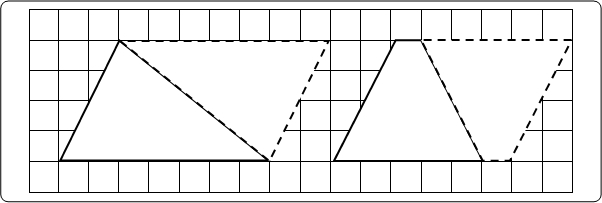



私の実践 私の工夫 算数 台形の面積 における導入問題の工夫 啓林館




台形の面積 数学が嫌いなんです



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典




数学 本質 三角形の面積の公式はなぜああなる そもそも面積とは Torm Note
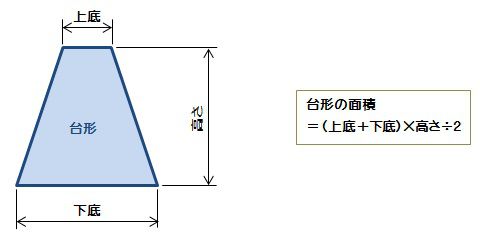



台形の面積 算数の公式覚えてますか
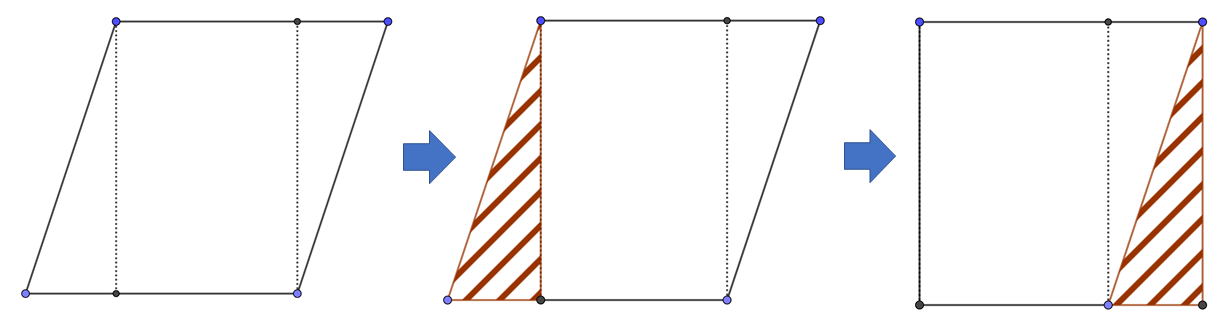



台形の面積が苦手 を克服する方法 中学受験ナビ




台形の面積の公式 算数の公式



Hamaguri Sakura Ne Jp Kakutyou Pdf




公式なんて覚えない ひし形の面積は直感的に考えよう
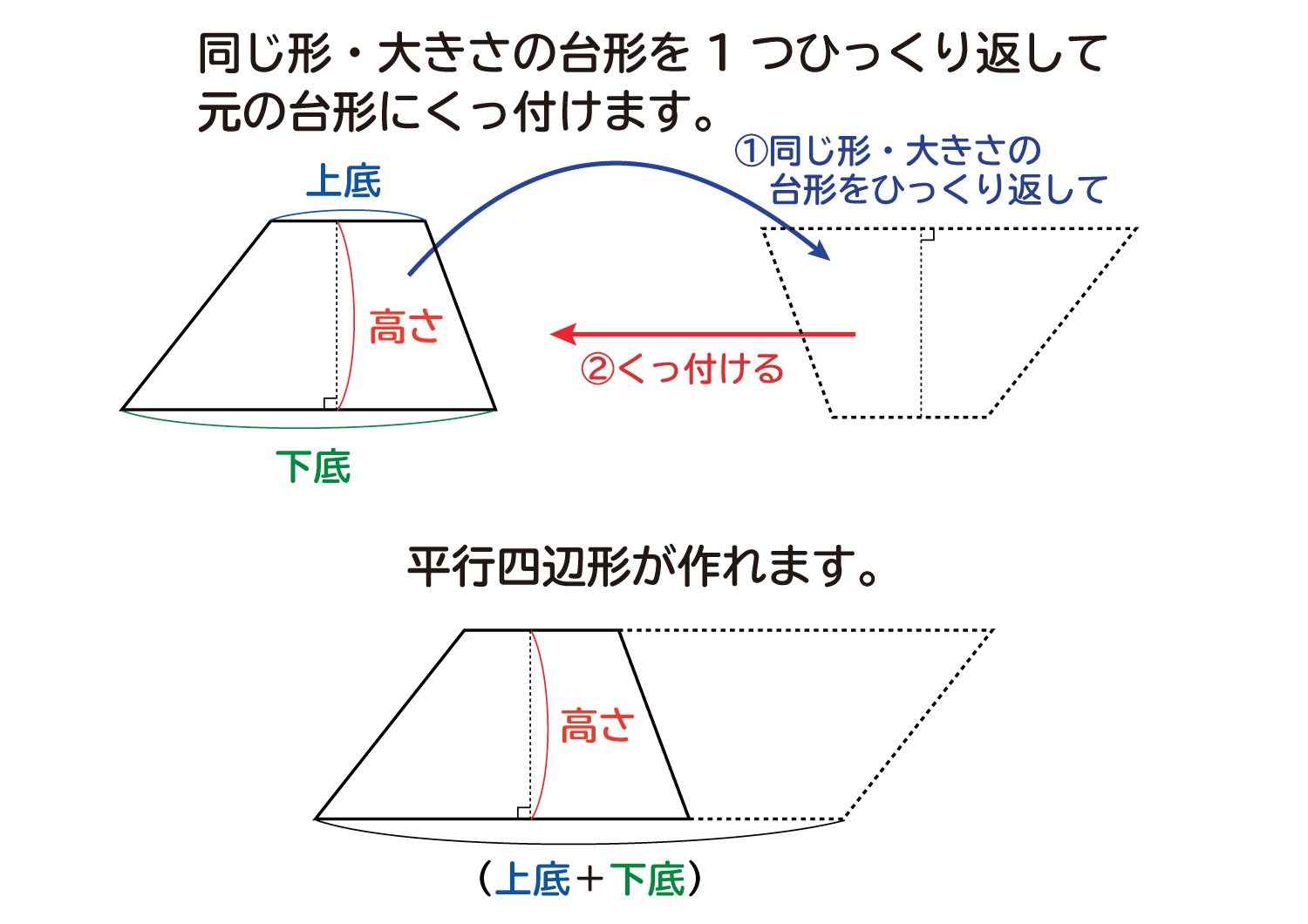



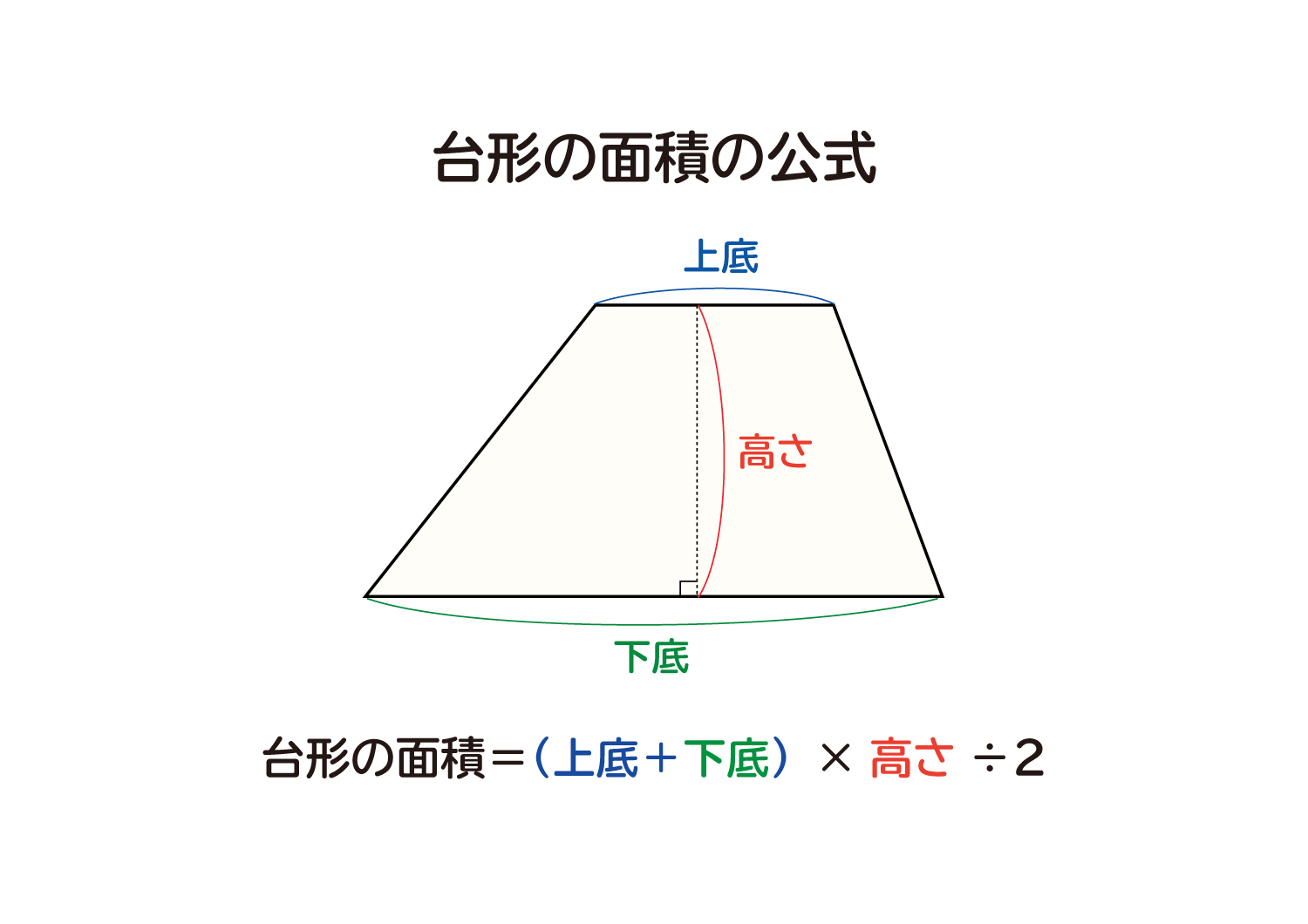
なぜ 台形の面積は 上底 下底 高さ 2 なのか を説明します おかわりドリル
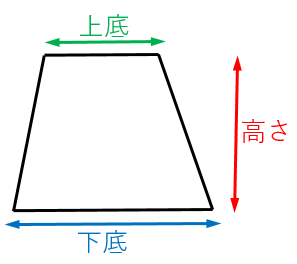



台形の面積を求める公式 具体例で学ぶ数学




三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学
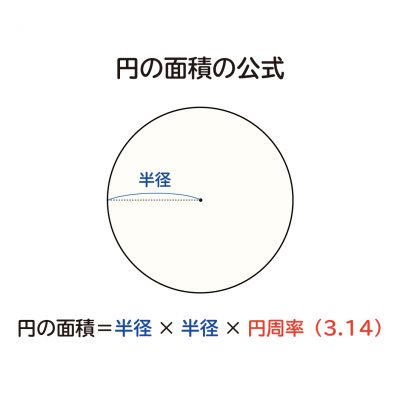



なぜ 台形の面積は 上底 下底 高さ 2 なのか を説明します おかわりドリル
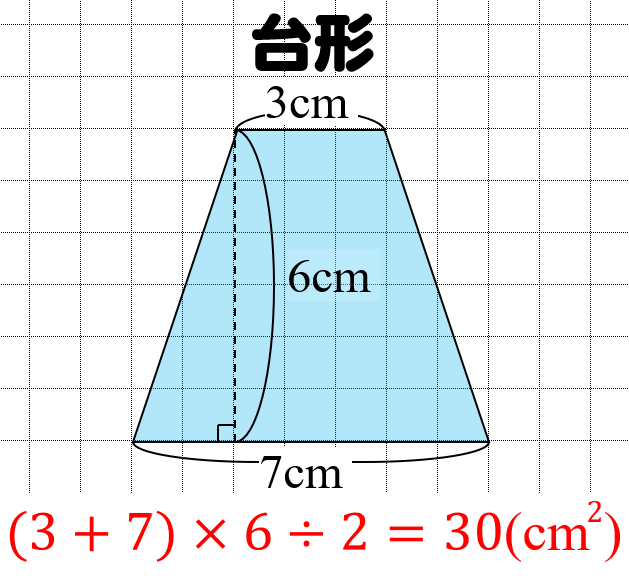



台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun
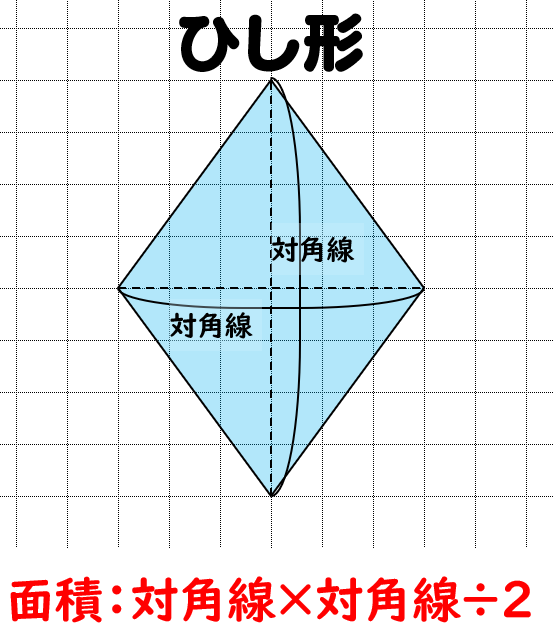



ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun
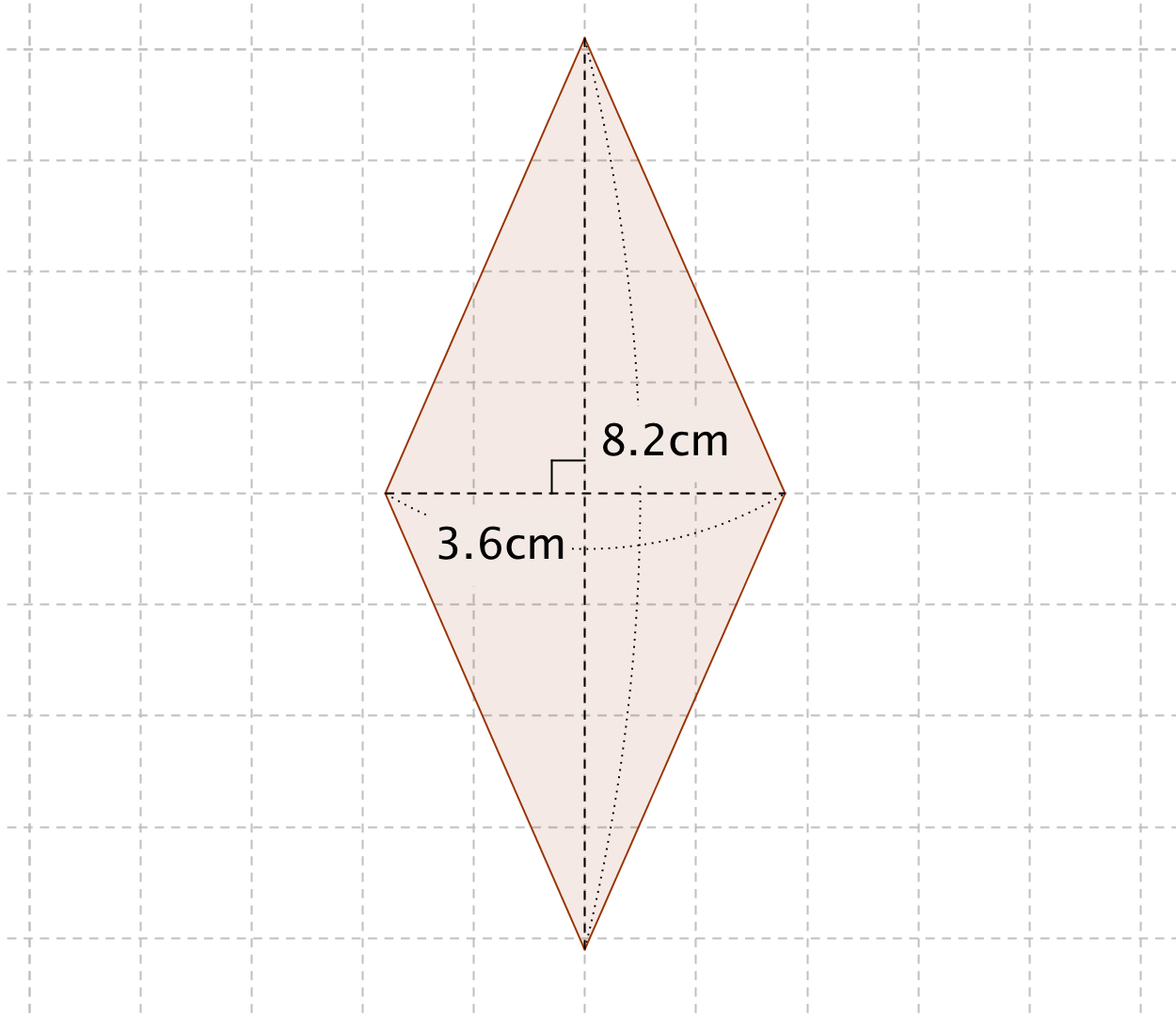



ひし形の面積の公式 算数の公式



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典
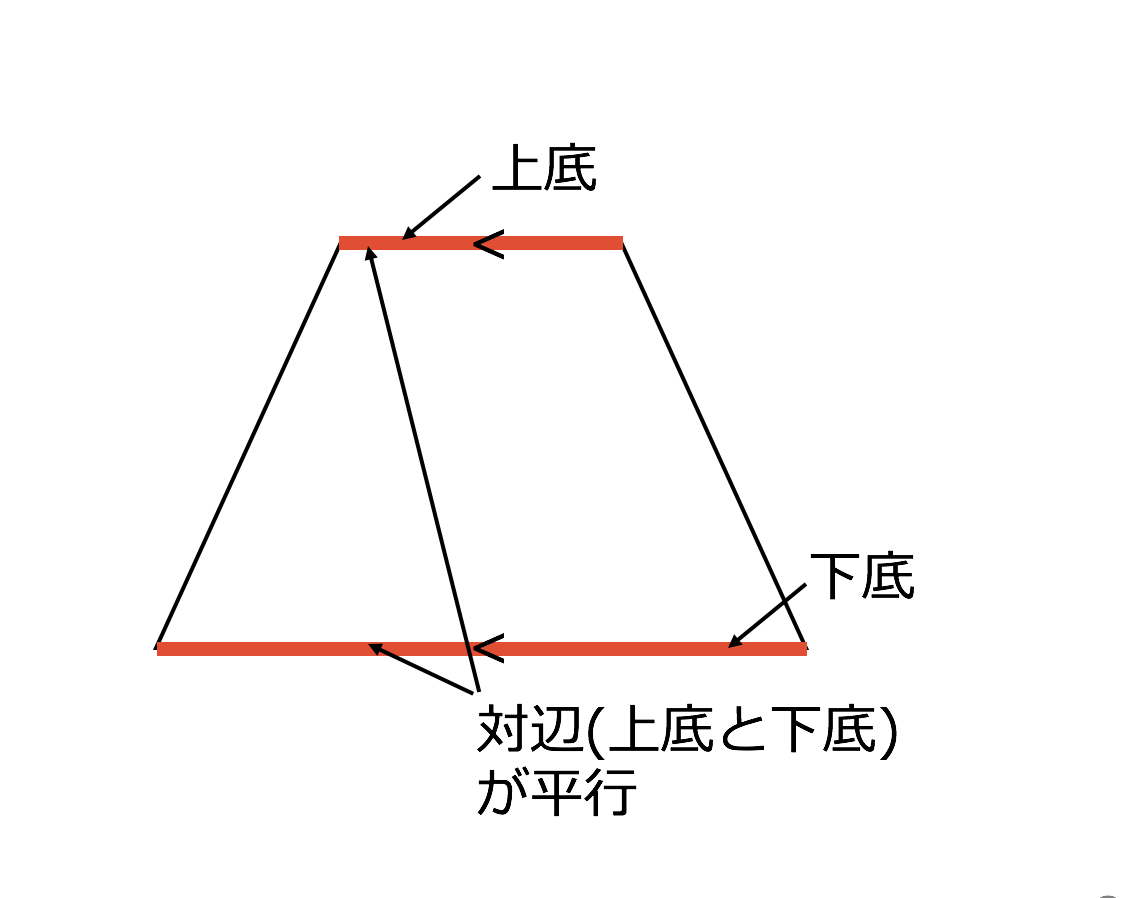



3分で分かる 台形の面積の求め方 公式についてわかりやすく 合格サプリ




高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
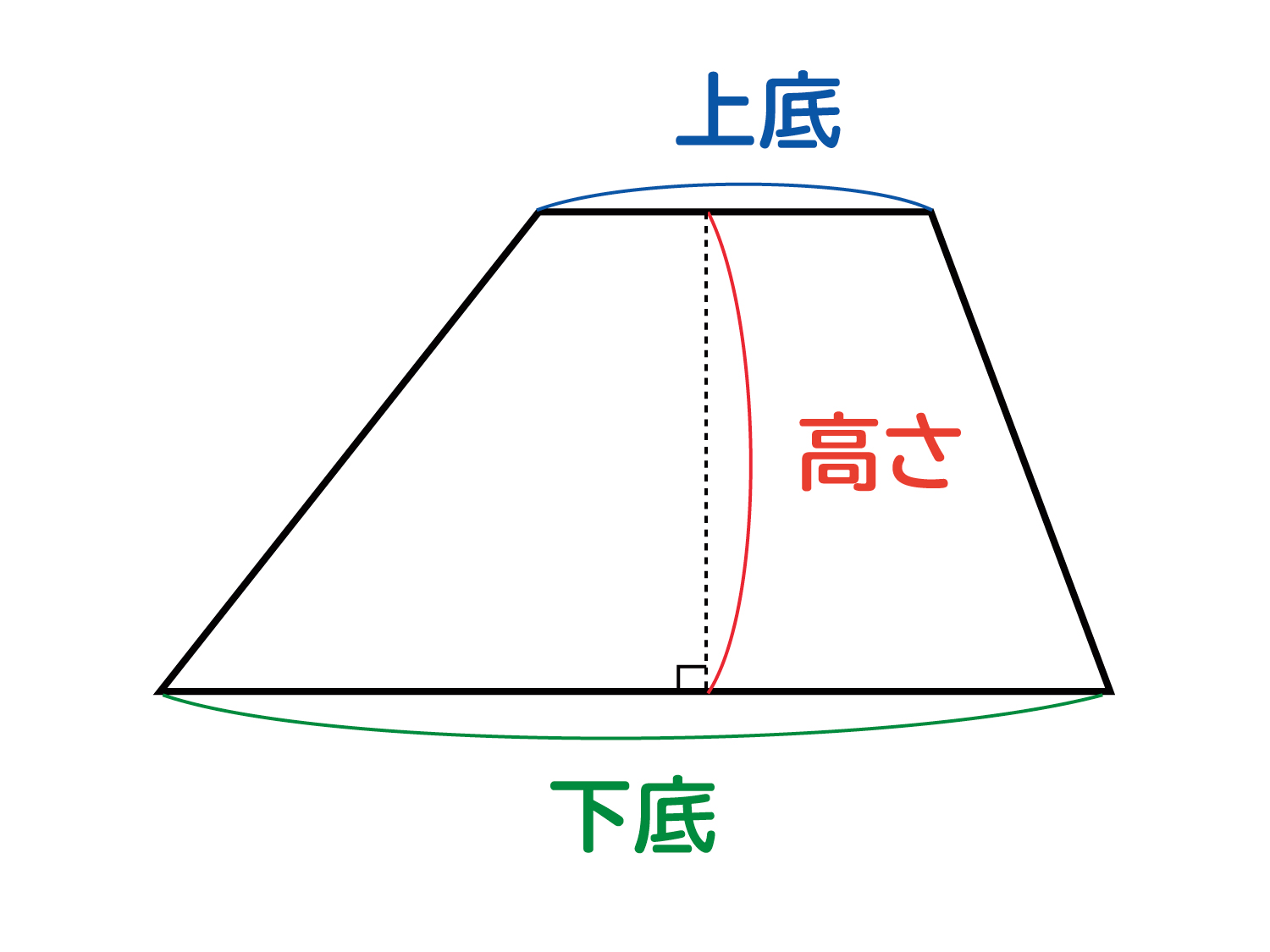



なぜ 台形の面積は 上底 下底 高さ 2 なのか を説明します おかわりドリル




四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




台形の面積の求め方 公式と計算例




簡単に面積が何倍か求められる 使える編 苦手な数学を簡単に




小学算数の面積の求め方と公式一覧 四角形 長方形の性質や円の計算方法まで解説 学びtimes




台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun




台形の面積の公式 Youtube



1
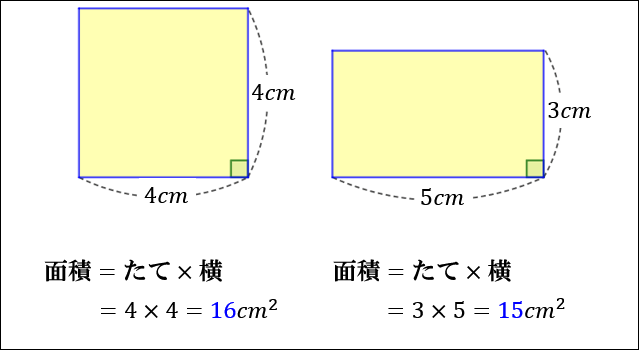



四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ



簡単公式 台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



ひし形の面積の公式 算数の公式



数学台形の公式がなぜ 上辺 下辺 高さ 2になるのかを証明 Yahoo 知恵袋




台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun




台形の面積の求めかたは 忘れても大丈夫 公式は自分でつくろう



なぜ 台形の面積は 上底 下底 高さ 2 なのか を説明します おかわりドリル



台形の底辺は 1分でわかる意味 計算 求め方 上辺 面積との関係



簡単公式 台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




台形の面積 における導入問題の工夫 三角形と台形の面積 どちらが大きい 私の実践 私の工夫アーカイブ一覧 授業支援 サポート資料 算数 小学校 知が啓く 教科書の啓林館



簡単に面積が何倍か求められる 使える編 苦手な数学を簡単に




三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学




図形の問題は公式の暗記に頼らないようにする まなびのへや
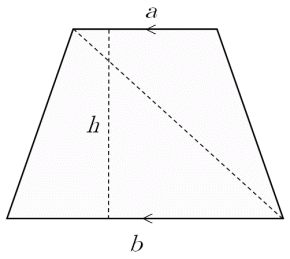



初等幾何 台形の面積はなぜ 上底 下底 高さ 2 なのか 大人が学び直す数学
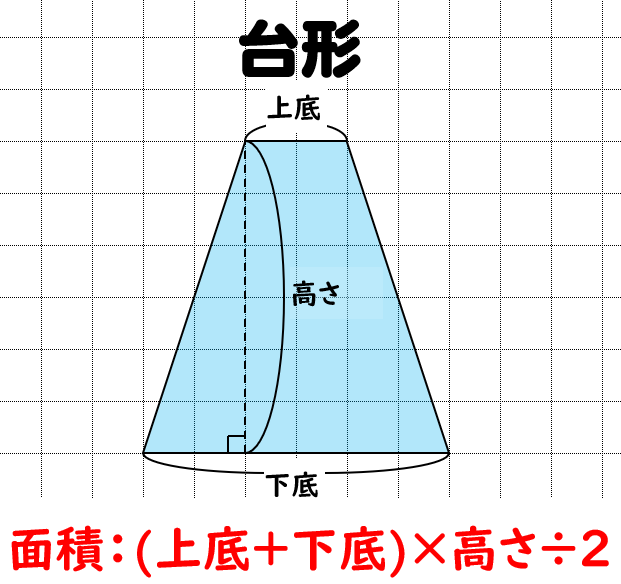



台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun



Q Tbn And9gcskqz Ppdvuumkcspdfklsb3r C5mohfuqvemohgl8suerhw5lr Usqp Cau



1
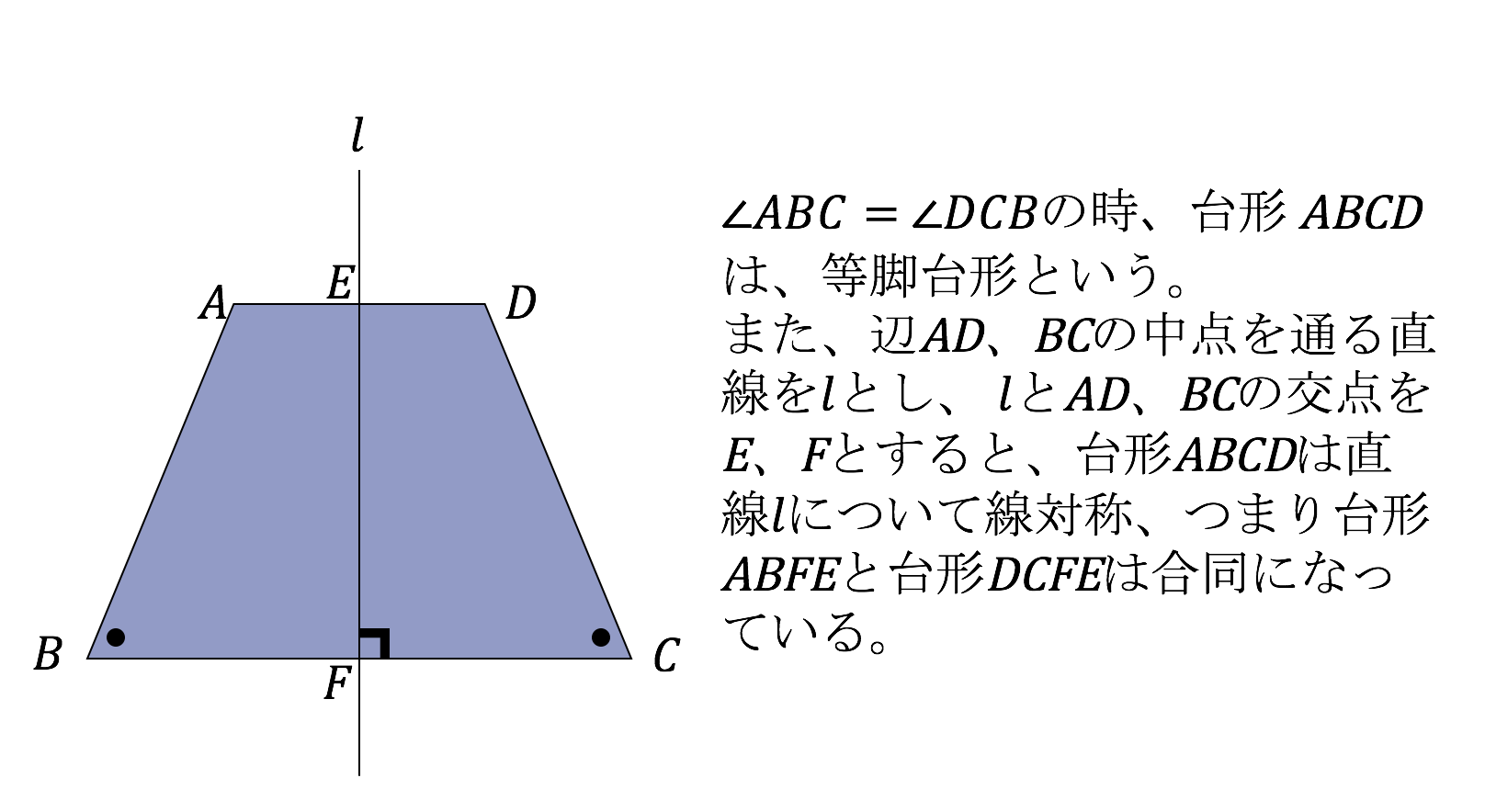



3分で分かる 台形の面積の求め方 公式についてわかりやすく 合格サプリ



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典




問題2の 2 について質問です なぜ 相似な図形の面積の比であるのに Clear




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ




補助線の引き方 日々の学習 兄中学受験




こちらの問題についてです Clear




台形の任意の高さにおける上辺の長さ 相似関係の2つの台形の高さがそれぞれ Okwave
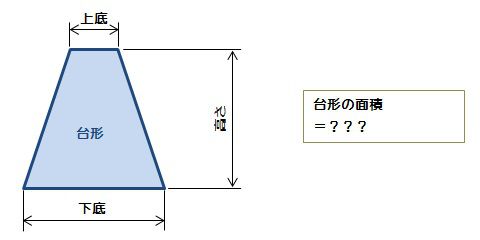



台形の面積 算数の公式覚えてますか
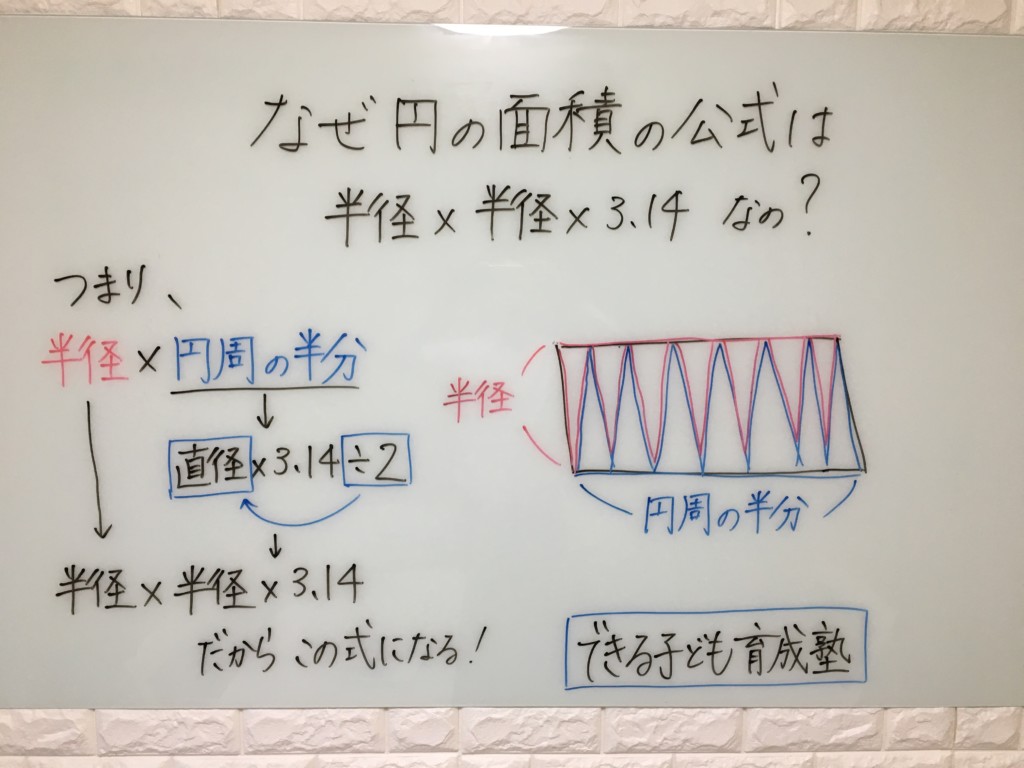



円の面積の求め方 公式 の理由を小学生に教える方法 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の小学生専門 国語と算数の苦手を克服
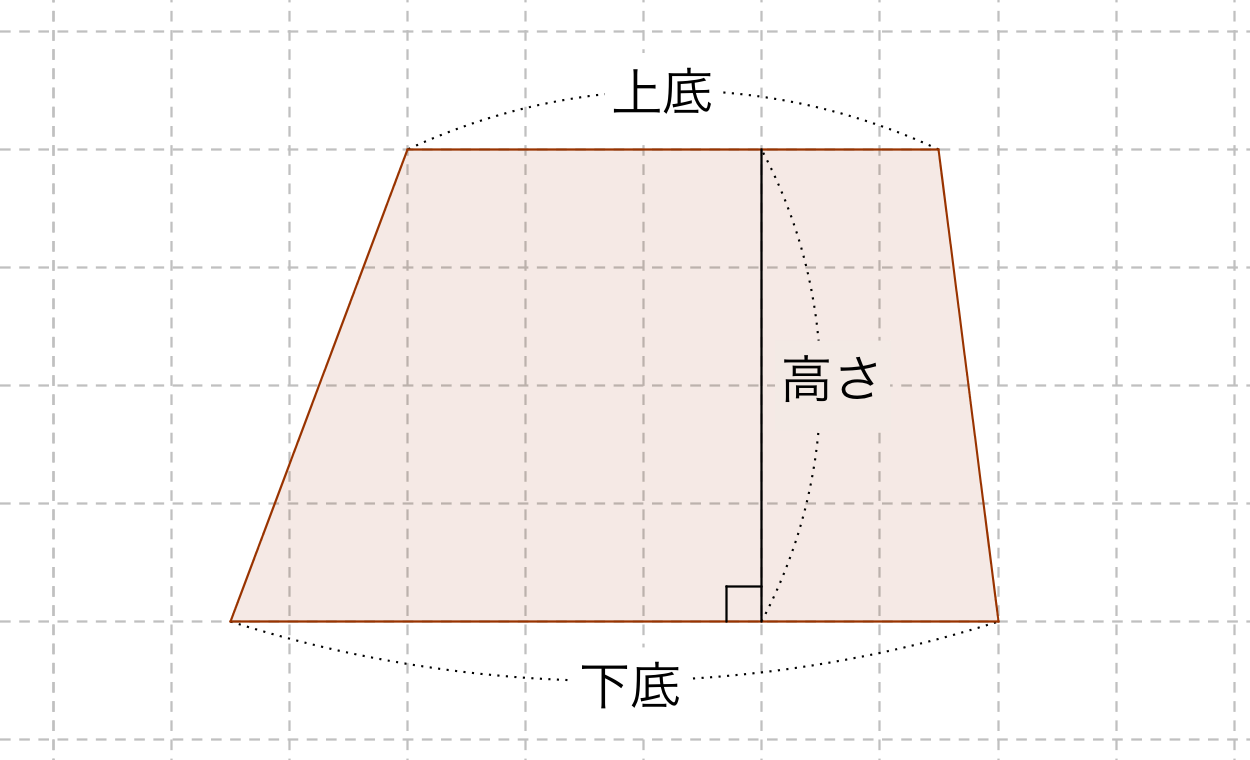



台形の面積の公式 算数の公式




台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun




台形の面積の求め方 公式と計算例



台形の面積はなぜ 2をするんでしょうか 詳しい方いたらお願いします 図の Yahoo 知恵袋
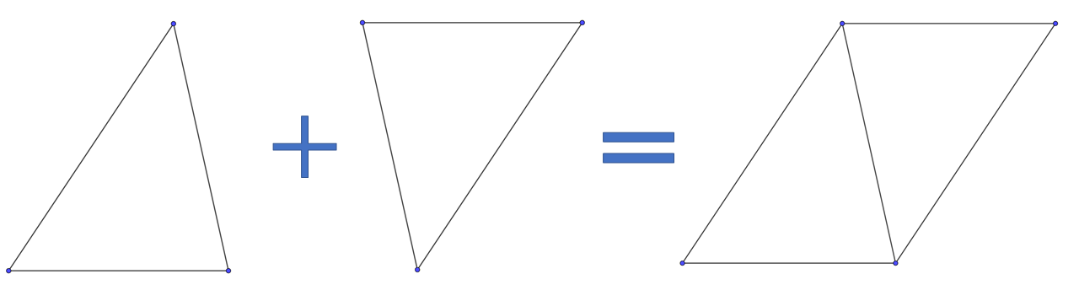



台形の面積が苦手 を克服する方法 中学受験ナビ
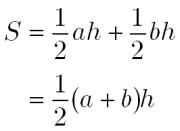



初等幾何 台形の面積はなぜ 上底 下底 高さ 2 なのか 大人が学び直す数学
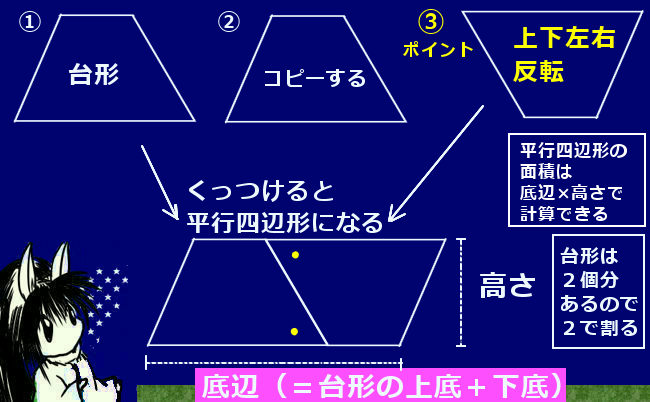



台形の面積公式 算数と図形 理数系無料オンライン学習 Kori




台形の面積の求め方 公式と計算例




5年算数 台形の面積 指導実践 ネコ好きな学校の先生の日常




台形の面積の求め方 公式が誰でも一目でわかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




3 1 はなぜ台形になりますか も分かりません Clear
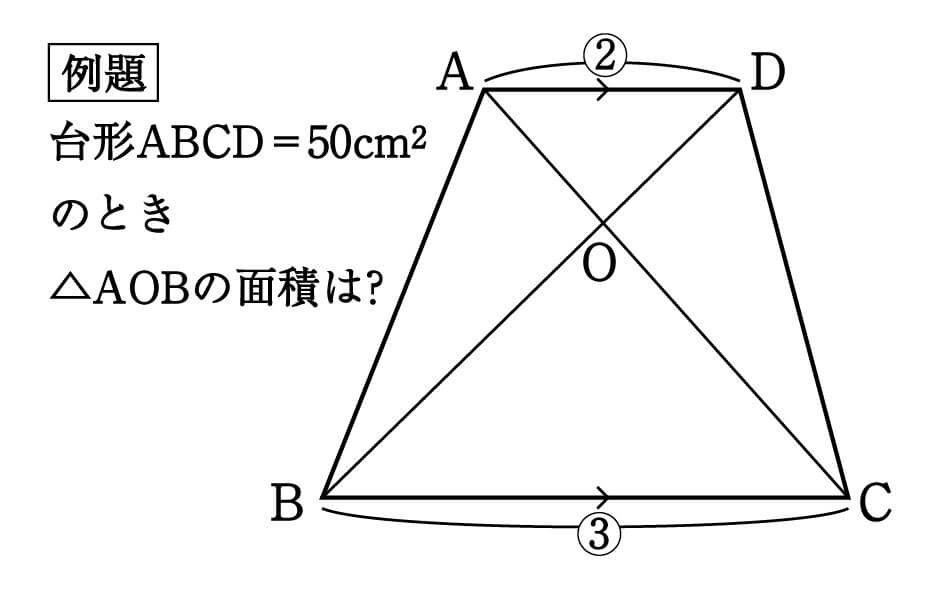



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
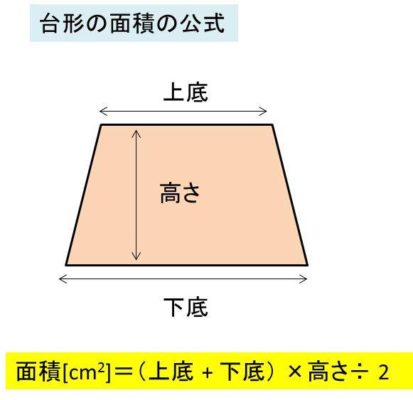



Excel エクセルで台形の面積を計算する方法 モッカイ




さかぽん先生 小5算 面積 台形1 公式だけ覚えてる人は要注意 なぜそうなるかも大事 Youtube



なぜ 台形の面積は 上底 下底 高さ 2 なのか を説明します おかわりドリル



だれか 台形の公式は なぜ 上底 下底 高さ 2になるのでしょ Yahoo 知恵袋
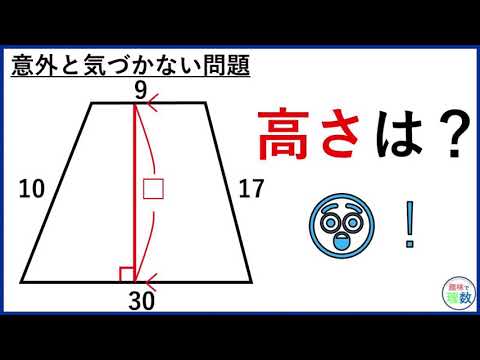



気づきにくい問題 台形の高さの求め方 Youtube
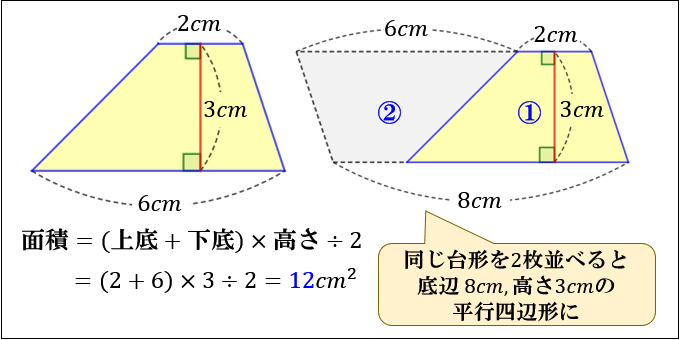



四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ




台形の 面積 底辺 角度 から 上辺と高さ の求め方 台形の面積 数学 教えて Goo
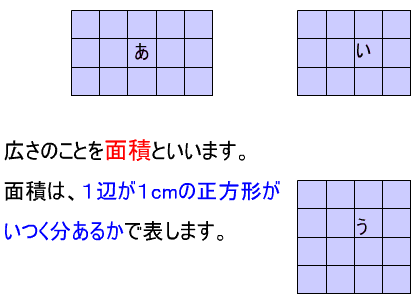



長方形の面積を求める公式の数学的な意味 Note Board




高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



熱の問題で この仕事を求めるとき右下の台形の面積が仕事になるのですが なぜ左上 Yahoo 知恵袋



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典



0 件のコメント:
コメントを投稿